Fit lasso (or elastic-net) penalized logistic regression for a Filebacked Big Matrix. Covariables can be added (/!\ penalized by default /!\).
big_spLogReg(
X,
y01.train,
ind.train = rows_along(X),
ind.col = cols_along(X),
covar.train = NULL,
base.train = NULL,
pf.X = NULL,
pf.covar = NULL,
alphas = 1,
power_scale = 1,
power_adaptive = 0,
K = 10,
ind.sets = NULL,
nlambda = 200,
nlam.min = 50,
n.abort = 10,
dfmax = 50000,
warn = TRUE,
ncores = 1,
...
)Arguments
- X
An object of class FBM.
- y01.train
Vector of responses, corresponding to
ind.train. Must be only 0s and 1s.- ind.train
An optional vector of the row indices that are used, for the training part. If not specified, all rows are used. Don't use negative indices.
- ind.col
An optional vector of the column indices that are used. If not specified, all columns are used. Don't use negative indices.
- covar.train
Matrix of covariables to be added in each model to correct for confounders (e.g. the scores of PCA), corresponding to
ind.train. Default isNULLand corresponds to only adding an intercept to each model. You can usecovar_from_df()to convert from a data frame.- base.train
Vector of base predictions. Model will be learned starting from these predictions. This can be useful if you want to previously fit a model with large-effect variables that you don't want to penalize.
- pf.X
A multiplicative factor for the penalty applied to each coefficient. If supplied,
pf.Xmust be a numeric vector of the same length asind.col. Default is all1. The purpose ofpf.Xis to apply differential penalization if some coefficients are thought to be more likely than others to be in the model. Setting SOME to 0 allows to have unpenalized coefficients.- pf.covar
Same as
pf.X, but forcovar.train. You might want to set some to 0 as variables with large effects can mask small effects in penalized regression.- alphas
The elastic-net mixing parameter that controls the relative contribution from the lasso (l1) and the ridge (l2) penalty. The penalty is defined as $$ \alpha||\beta||_1 + (1-\alpha)/2||\beta||_2^2.$$
alpha = 1is the lasso penalty andalphain between0(1e-4) and1is the elastic-net penalty. Default is1. You can pass multiple values, and only one will be used (optimized by grid-search).- power_scale
When using lasso (alpha = 1), penalization to apply that is equivalent to scaling genotypes dividing by (standard deviation)^power_scale. Default is 1 and corresponding to standard scaling. Using 0 would correspond to using unscaled variables and using 0.5 is Pareto scaling. If you e.g. use
power_scale = c(0, 0.5, 1), the best value in CMSA will be used (just like withalphas).- power_adaptive
Multiplicative penalty factor to apply to variables in the form of 1 / m_j^power_adaptive, where m_j is the marginal statistic for variable j. Default is 0, which effectively disables this option. If you e.g. use
power_adaptive = c(0, 0.5, 1.5), the best value in CMSA will be used (just like withalphas).- K
Number of sets used in the Cross-Model Selection and Averaging (CMSA) procedure. Default is
10.- ind.sets
Integer vectors of values between
1andKspecifying which set each index of the training set is in. Default randomly assigns these values but it can be useful to set this vector for reproducibility, or if you want to refine the grid-search overalphasusing the same sets.- nlambda
The number of lambda values. Default is
200.- nlam.min
Minimum number of lambda values to investigate. Default is
50.- n.abort
Number of lambda values for which prediction on the validation set must decrease before stopping. Default is
10.- dfmax
Upper bound for the number of nonzero coefficients. Default is
50e3because, for large data sets, computational burden may be heavy for models with a large number of nonzero coefficients.- warn
Whether to warn if some models may not have reached a minimum. Default is
TRUE.- ncores
Number of cores used. Default doesn't use parallelism. You may use nb_cores.
- ...
Arguments passed on to
COPY_biglasso_mainlambda.min.ratioThe smallest value for lambda, as a fraction of lambda.max. Default is
.0001if the number of observations is larger than the number of variables and.001otherwise.epsConvergence threshold for inner coordinate descent. The algorithm iterates until the maximum change in the objective after any coefficient update is less than
epstimes the null deviance. Default value is1e-5.max.iterMaximum number of iterations. Default is
1000.return.allDeprecated. Now always return all models.
Value
Return an object of class big_sp_list (a list of length(alphas)
x K) that has 3 methods predict, summary and plot.
Details
This is a modified version of one function of
package biglasso.
It adds the possibility to train models with covariables and use many
types of FBM (not only double ones).
Yet, it only corresponds to screen = "SSR" (Sequential Strong Rules).
Also, to remove the choice of the lambda parameter, we introduce the Cross-Model Selection and Averaging (CMSA) procedure:
This function separates the training set in
Kfolds (e.g. 10).In turn,
each fold is considered as an inner validation set and the others (K - 1) folds form an inner training set,
the model is trained on the inner training set and the corresponding predictions (scores) for the inner validation set are computed,
the vector of scores which maximizes log-likelihood is determined,
the vector of coefficients corresponding to the previous vector of scores is chosen.
The
Kresulting vectors of coefficients are then averaged into one final vector of coefficients.
References
Tibshirani, R., Bien, J., Friedman, J., Hastie, T., Simon, N., Taylor, J. and Tibshirani, R. J. (2012), Strong rules for discarding predictors in lasso-type problems. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 74: 245-266. doi:10.1111/j.1467-9868.2011.01004.x .
Zeng, Y., and Breheny, P. (2017). The biglasso Package: A Memory- and Computation-Efficient Solver for Lasso Model Fitting with Big Data in R. doi:10.32614/RJ-2021-001 .
Privé, F., Aschard, H., and Blum, M. G.B. (2019). Efficient implementation of penalized regression for genetic risk prediction. Genetics, 212: 65-74. doi:10.1534/genetics.119.302019 .
See also
Examples
set.seed(2)
# simulating some data
N <- 230
M <- 730
X <- FBM(N, M, init = rnorm(N * M, sd = 5))
y01 <- as.numeric((rowSums(X[, 1:10]) + 2 * rnorm(N)) > 0)
covar <- matrix(rnorm(N * 3), N)
ind.train <- sort(sample(nrow(X), 150))
ind.test <- setdiff(rows_along(X), ind.train)
# fitting model for multiple lambdas and alphas
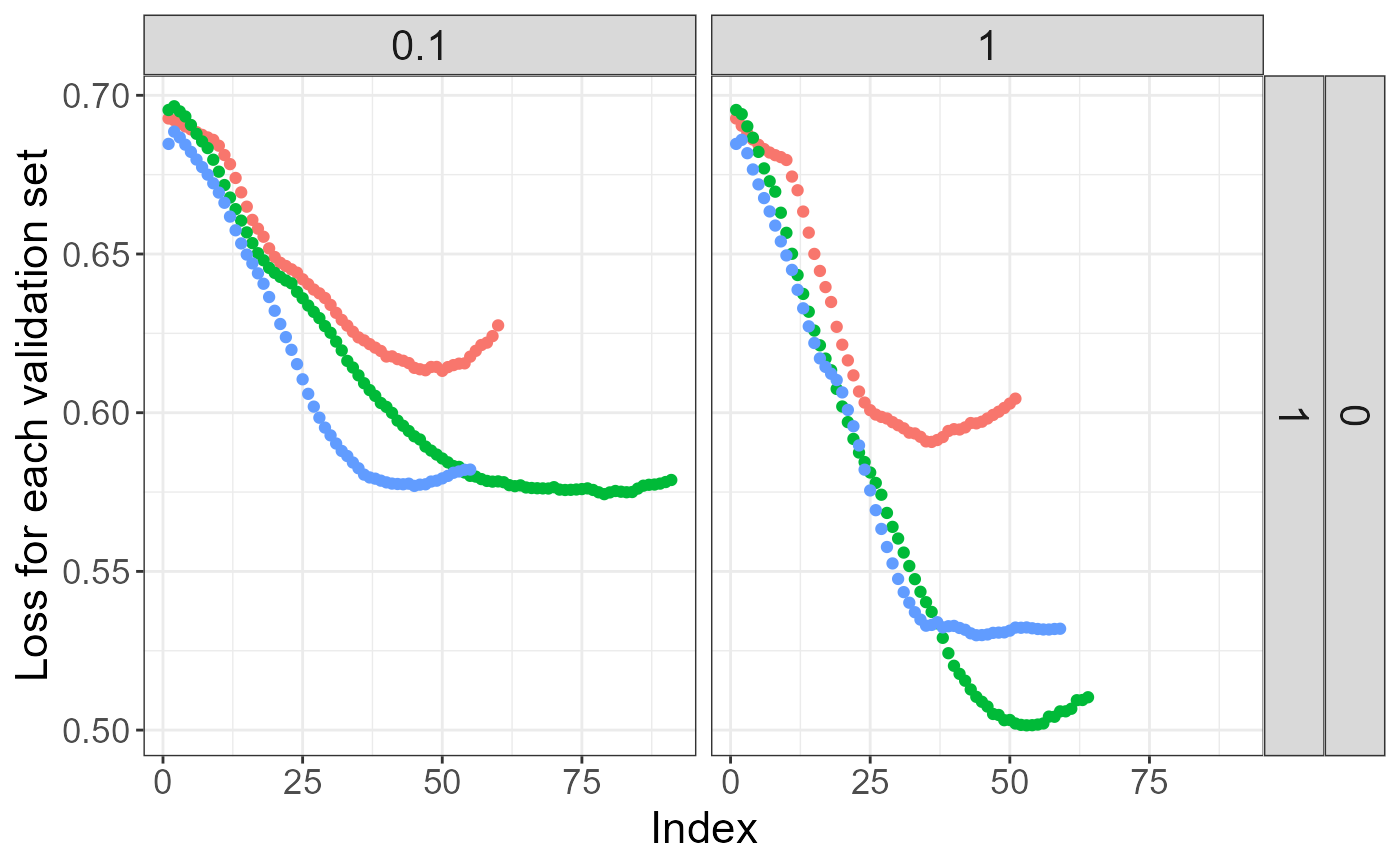
test <- big_spLogReg(X, y01[ind.train], ind.train = ind.train,
covar.train = covar[ind.train, ],
alphas = c(1, 0.1), K = 3, warn = FALSE)
# peek at the models
plot(test)
 summary(test, sort = TRUE)
#> # A tibble: 2 × 9
#> alpha power_adaptive power_scale validation_loss intercept beta nb_var
#> <dbl> <dbl> <dbl> <dbl> <dbl> <list> <int>
#> 1 1 0 1 0.541 0.113 <dbl [733]> 99
#> 2 0.1 0 1 0.588 0.123 <dbl [733]> 158
#> # ℹ 2 more variables: message <list>, all_conv <lgl>
summary(test, sort = TRUE)$message
#> [[1]]
#> [1] "No more improvement" "No more improvement" "No more improvement"
#>
#> [[2]]
#> [1] "No more improvement" "No more improvement" "No more improvement"
#>
# prediction for other data -> only the best alpha is used
summary(test, best.only = TRUE)
#> # A tibble: 1 × 9
#> alpha power_adaptive power_scale validation_loss intercept beta nb_var
#> <dbl> <dbl> <dbl> <dbl> <dbl> <list> <int>
#> 1 1 0 1 0.541 0.113 <dbl [733]> 99
#> # ℹ 2 more variables: message <list>, all_conv <lgl>
pred <- predict(test, X, ind.row = ind.test, covar.row = covar[ind.test, ])
AUC(pred, y01[ind.test])
#> [1] 0.8232323
library(ggplot2)
#> Warning: package 'ggplot2' was built under R version 4.2.3
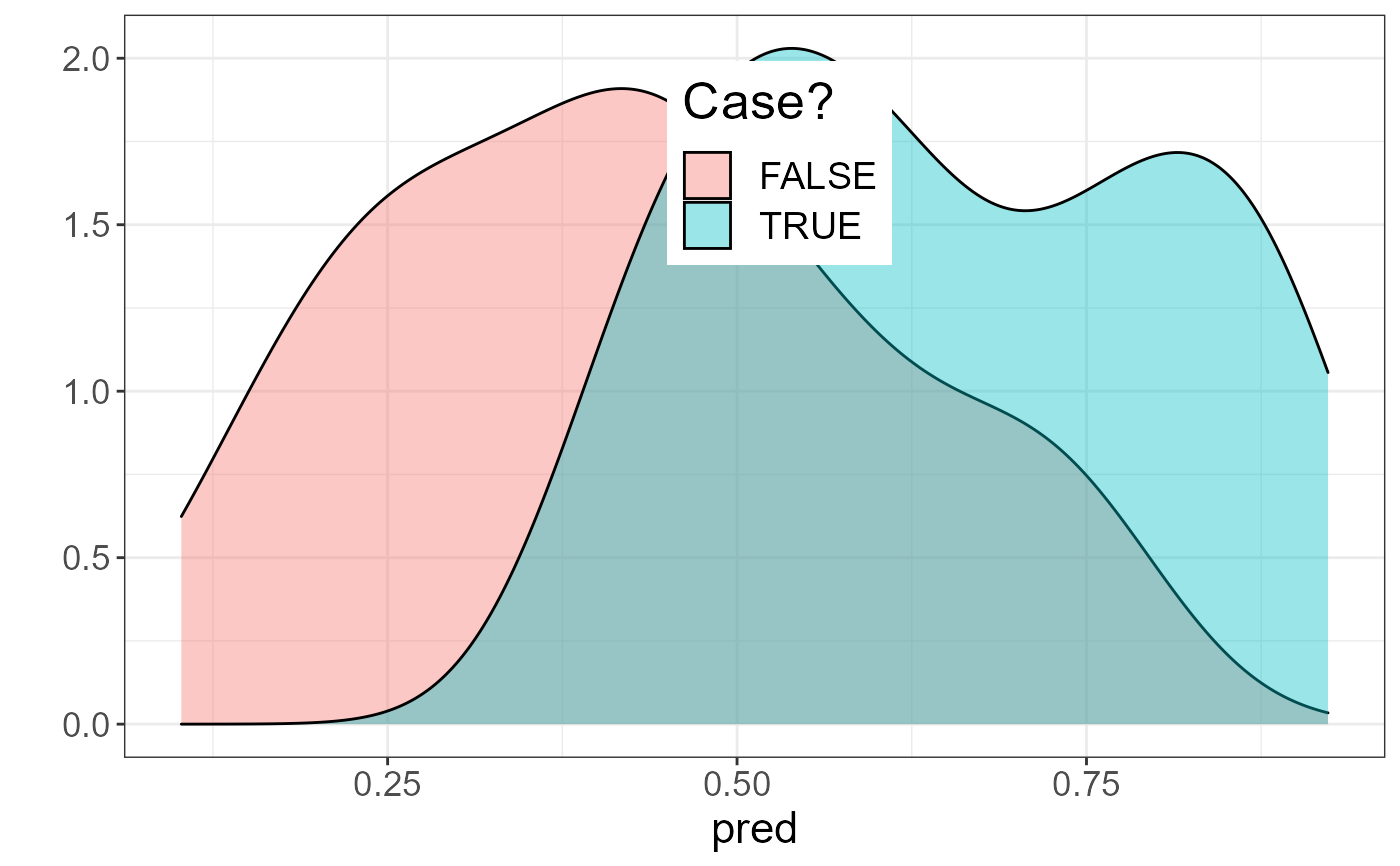
qplot(pred, fill = as.logical(y01[ind.test]),
geom = "density", alpha = I(0.4)) +
labs(fill = "Case?") +
theme_bigstatsr() +
theme(legend.position = c(0.52, 0.8))
#> Warning: `qplot()` was deprecated in ggplot2 3.4.0.
#> Warning: A numeric `legend.position` argument in `theme()` was deprecated in ggplot2
#> 3.5.0.
#> ℹ Please use the `legend.position.inside` argument of `theme()` instead.
summary(test, sort = TRUE)
#> # A tibble: 2 × 9
#> alpha power_adaptive power_scale validation_loss intercept beta nb_var
#> <dbl> <dbl> <dbl> <dbl> <dbl> <list> <int>
#> 1 1 0 1 0.541 0.113 <dbl [733]> 99
#> 2 0.1 0 1 0.588 0.123 <dbl [733]> 158
#> # ℹ 2 more variables: message <list>, all_conv <lgl>
summary(test, sort = TRUE)$message
#> [[1]]
#> [1] "No more improvement" "No more improvement" "No more improvement"
#>
#> [[2]]
#> [1] "No more improvement" "No more improvement" "No more improvement"
#>
# prediction for other data -> only the best alpha is used
summary(test, best.only = TRUE)
#> # A tibble: 1 × 9
#> alpha power_adaptive power_scale validation_loss intercept beta nb_var
#> <dbl> <dbl> <dbl> <dbl> <dbl> <list> <int>
#> 1 1 0 1 0.541 0.113 <dbl [733]> 99
#> # ℹ 2 more variables: message <list>, all_conv <lgl>
pred <- predict(test, X, ind.row = ind.test, covar.row = covar[ind.test, ])
AUC(pred, y01[ind.test])
#> [1] 0.8232323
library(ggplot2)
#> Warning: package 'ggplot2' was built under R version 4.2.3
qplot(pred, fill = as.logical(y01[ind.test]),
geom = "density", alpha = I(0.4)) +
labs(fill = "Case?") +
theme_bigstatsr() +
theme(legend.position = c(0.52, 0.8))
#> Warning: `qplot()` was deprecated in ggplot2 3.4.0.
#> Warning: A numeric `legend.position` argument in `theme()` was deprecated in ggplot2
#> 3.5.0.
#> ℹ Please use the `legend.position.inside` argument of `theme()` instead.