Tip: Optimize your Rcpp loops
In this post, I will show you how to optimize your Rcpp loops so that they are 2 to 3 times faster than a standard implementation.
Context
Real data example
For this post, I will use a big.matrix which represents genotypes for 15,283 individuals, corresponding to the number of mutations (0, 1 or 2) at 287,155 different loci. Here, I will use only the first 10,000 loci (columns).
What you need to know about the big.matrix format:
- you can easily and quickly access matrice-like objects stored on disk,
- you can use different types of storage (I use type
charto store each element on only 1 byte), - it is column-major ordered as standard
Rmatrices, - you can access elements of a
big.matrixusingX[i, j]inR, - you can access elements of a
big.matrixusingX[j][i]inRcpp, - you can get a
RcppEigenorRcppArmadilloview of abig.matrix(see Appendix). - for more details, go to the GitHub repo.
Peek at the data:
print(dim(X))## [1] 15283 10000print(X[1:10, 1:12])## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## [1,] 2 0 2 0 2 2 2 1 2 2 2 2
## [2,] 2 0 1 2 1 1 1 1 2 1 2 2
## [3,] 2 0 2 2 2 2 1 1 2 1 2 2
## [4,] 2 2 0 2 0 0 0 2 2 2 0 2
## [5,] 2 1 2 2 2 2 2 1 2 2 2 2
## [6,] 2 1 2 1 2 2 1 1 2 2 2 2
## [7,] 2 0 2 0 2 2 2 0 2 1 2 2
## [8,] 2 1 1 2 1 1 1 1 2 1 2 2
## [9,] 2 1 2 2 2 2 2 2 2 2 2 2
## [10,] 2 0 2 1 2 2 2 0 2 1 2 1What I needed
I needed a fast matrix-vector multiplication between a big.matrix and a vector. Moreover, I could not use any RcppEigen or RcppArmadillo multiplication because I needed some options of efficiently subsetting columns or rows in my matrix (see Appendix).
Writing this multiplication in Rcpp is no more than two loops:
// [[Rcpp::depends(RcppEigen, bigmemory, BH)]]
#include <RcppEigen.h>
#include <bigmemory/MatrixAccessor.hpp>
using namespace Rcpp;
// [[Rcpp::export]]
NumericVector prod1(XPtr<BigMatrix> bMPtr, const NumericVector& x) {
MatrixAccessor<char> macc(*bMPtr);
int n = bMPtr->nrow();
int m = bMPtr->ncol();
NumericVector res(n);
int i, j;
for (j = 0; j < m; j++) {
for (i = 0; i < n; i++) {
res[i] += macc[j][i] * x[j];
}
}
return res;
}One test:
y <- rnorm(ncol(X))
print(system.time(
test <- prod1(X@address, y)
))## user system elapsed
## 0.664 0.004 0.668What comes next should be transposable to other applications and other types of data.
Unrolling optimization
While searching for optimizing my multiplication, I came across this Stack Overflow answer.
Unrolling in action:
// [[Rcpp::depends(RcppEigen, bigmemory, BH)]]
#include <RcppEigen.h>
#include <bigmemory/MatrixAccessor.hpp>
using namespace Rcpp;
// [[Rcpp::export]]
NumericVector prod4(XPtr<BigMatrix> bMPtr, const NumericVector& x) {
MatrixAccessor<char> macc(*bMPtr);
int n = bMPtr->nrow();
int m = bMPtr->ncol();
NumericVector res(n);
int i, j;
for (j = 0; j <= m - 4; j += 4) {
for (i = 0; i < n; i++) { // unrolling optimization
res[i] += (x[j] * macc[j][i] + x[j+1] * macc[j+1][i]) +
(x[j+2] * macc[j+2][i] + x[j+3] * macc[j+3][i]);
} // The parentheses are somehow important. Try without.
}
for (; j < m; j++) {
for (i = 0; i < n; i++) {
res[i] += x[j] * macc[j][i];
}
}
return res;
}require(microbenchmark)
print(microbenchmark(
PROD1 = test1 <- prod1(X@address, y),
PROD4 = test2 <- prod4(X@address, y),
times = 5
))## Unit: milliseconds
## expr min lq mean median uq max neval
## PROD1 609.0916 612.6428 613.7418 613.3740 616.4907 617.1096 5
## PROD4 262.2658 267.7352 267.0268 268.0026 268.0785 269.0521 5print(all.equal(test1, test2))## [1] TRUENice! Let’s try more. Why not using 8 or 16 rather than 4?
Rcpp::sourceCpp('https://privefl.github.io/blog/code/prods.cpp')
print(bench <- microbenchmark(
PROD1 = prod1(X@address, y),
PROD2 = prod2(X@address, y),
PROD4 = prod4(X@address, y),
PROD8 = prod8(X@address, y),
PROD16 = prod16(X@address, y),
times = 5
))## Unit: milliseconds
## expr min lq mean median uq max neval
## PROD1 620.9375 627.9209 640.6087 631.1818 659.4236 663.5798 5
## PROD2 407.6275 418.1752 417.1746 418.4589 419.0665 422.5451 5
## PROD4 267.1687 271.4726 283.1928 271.9553 279.6698 325.6979 5
## PROD8 241.5542 242.9120 255.4974 246.5218 267.7683 278.7307 5
## PROD16 212.4335 213.5228 217.4781 217.1801 221.5119 222.7423 5time <- summary(bench)[, "median"]
step <- 2^(0:4)
plot(step, time, type = "b", xaxt = "n", yaxt = "n",
xlab = "size of each step")
axis(side = 1, at = step)
axis(side = 2, at = round(time))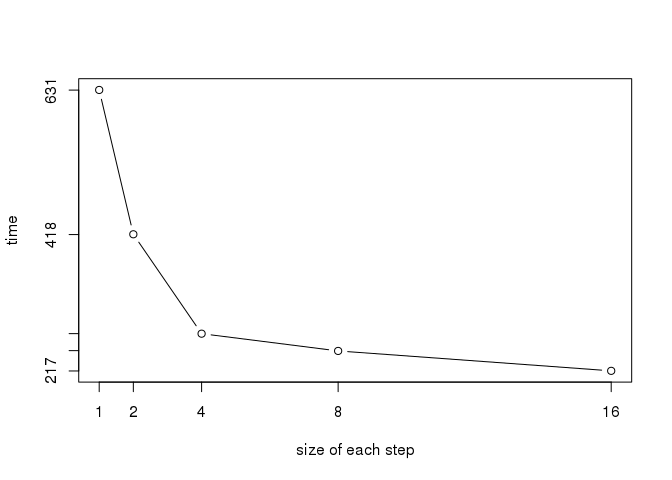
Conclusion
We have seen that unrolling can dramatically improve performances on loops. Steps of size 8 or 16 are of relatively little extra gain compared to 2 or 4.
As pointed out in the SO answer, it can behave rather differently between systems. So, if it is for your personal use, use the maximum gain (try 32!), but as I want my function to be used by others in a package, I think it’s safer to choose a step of 4.
Appendix
You can do a big.matrix-vector multiplication easily with RcppEigen or RcppArmadillo (see this code) but it lacks of efficient subsetting option.
Indeed, you still can’t use subsetting in Eigen, but this will come as said in this feature request. For Armadillo, you can but it is rather slow:
Rcpp::sourceCpp('https://privefl.github.io/blog/code/prods2.cpp')
n <- nrow(X)
ind <- sort(sample(n, size = n/2))
print(microbenchmark(
EIGEN = test3 <- prodEigen(X@address, y),
ARMA = test4 <- prodArma(X@address, y),
ARMA_SUB = test5 <- prodArmaSub(X@address, y, ind - 1),
times = 5
))## Unit: milliseconds
## expr min lq mean median uq max neval
## EIGEN 567.5607 570.1843 717.2433 572.9402 576.2028 1299.3285 5
## ARMA 1242.3581 1263.8803 1329.1212 1264.7070 1284.5612 1590.0993 5
## ARMA_SUB 455.1174 457.5862 466.3982 461.5883 465.9056 491.7935 5print(all(
all.equal(test3, test),
all.equal(as.numeric(test4), test),
all.equal(as.numeric(test5), test[ind])
))## [1] TRUE