One year as a subscriber to Stack Overflow

Written on July 2, 2018

In this post, I follow up on a previous post describing how last year in July, I spent one month mostly procrastinating on Stack Overflow (SO). We’re already in July so it’s time to get back to one year of activity on Stack Overflow.

Am I still as much active as before? What is my strategy for answering questions on SO?

My activity on Stack Overflow

Again, we’ll use David Robinson’s package {stackr} to get data from Stack Overflow API in R.

# devtools::install_github("dgrtwo/stackr")
suppressMessages({
  library(stackr)
  library(tidyverse)
  library(lubridate)
})

Evolution of my SO reputation

myID <- "6103040"

myRep <- stack_users(myID, "reputation-history", num_pages = 40,
                     fromdate = today() - years(1))

myRep %>%
  arrange(creation_date) %>%
  ggplot(aes(creation_date, cumsum(reputation_change))) +
  geom_point() +
  labs(x = "Date", y = "Reputation (squared transformed)",
       title = "Evolution of my SO reputation over the last year") + 
  bigstatsr::theme_bigstatsr()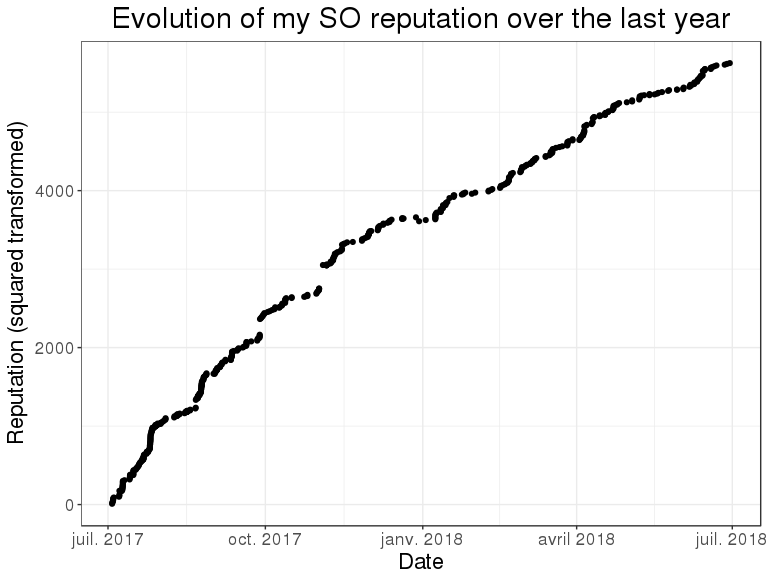

So, it seems that my activity is slowing gently (my reputation is almost proportional to the square root of time). Yet, it is still increasing steadily; so what is my strategy for answering questions on SO?

Tags I’m involved in

You’ll have to wait for the answer to what is my strategy for answering questions on SO. For a hint, let’s analyze the tags I’m involved in.

If we don’t count my first month of activity:

stack_users(myID, "tags", num_pages = 40,
            fromdate = today() - months(11)) %>%
  select(name, count) %>%
  as_tibble()

## # A tibble: 155 x 2
##    name                count
##    <chr>               <int>
##  1 r                     187
##  2 performance            36
##  3 rcpp                   34
##  4 parallel-processing    33
##  5 foreach                19
##  6 r-bigmemory            14
##  7 vectorization          12
##  8 for-loop               11
##  9 matrix                 11
## 10 doparallel             10
## # ... with 145 more rows

I’m obviously answering only R questions. The tags I’m mostly answering questions from are “performance”, “rcpp”, “parallel-processing”, “foreach”, “r-bigmemory” and “vectorization”.

Performance

As you can see, all these tags are about performance of code. I really enjoy performance problems (get the same result but much faster).

I can spend hours on a question about performance and am sometimes rewarded with a solution that is 2-3 order of magnitude faster (see e.g. this other post).

I hope I could share my knowledge about performance through a tutorial in Toulouse next year.

Conclusion and answer

So, the question was “What is my strategy for answering questions on SO?”. And the answer is.. in the title: I am a subscriber.

I subscribe to tags on Stack Overflow. It has many benefits:

you don’t have to rush to answer because questions you receive by mail are 30min-old (unanswered?) ones, so the probability that someone will answer at the same time as you is low.
you can focus and what you’re good at, what you’re interested in, or just what you want to learn. For example, I subscribed to the very new tag “r-future” (for the R package {future}) because I’m interested in this package, even if I don’t know how to use it yet. I had the chance to meet with its author, Henrik Bengtsson, at eRum2018 and he actually already knew me through parallel questions on SO :D.

However, some tags (like “performance” or “foreach”) are relevant to many programming languages so that you would be flooded with irrelevant questions if subscribing directly to these tags. A simple solution to this problem is to subscribe to a feed of a combination of tags, like https://stackoverflow.com/feeds/tag?tagnames=r+and+foreach&sort=newest. I use this website to subscribe to feeds.

I will continue answering questions on SO, so see you there!

PS: I’m not sure you would get only unanswered questions with this technique.