Performance: when algorithmics meets mathematics

Written on April 19, 2018

In this post, I talk about performance through an efficient algorithm I developed for finding closest points on a map. This algorithm uses both concepts from mathematics and algorithmics.

Problem to solve

This problem comes from a recent question on StackOverflow.

I have two matrices, one is 200K rows long, the other is 20K. For each row (which is a point) in the first matrix, I am trying to find which row (also a point) in the second matrix is closest to the point in the first matrix. This is the first method that I tried on a sample dataset:

# Test dataset: longitude and latitude
pixels.latlon <- cbind(runif(200000, min = -180, max = -120),
                       runif(200000, min = 50, max = 85))
grwl.latlon <- cbind(runif(20000, min = -180, max = -120),
                     runif(20000, min = 50, max = 85))
# Calculate the distance matrix
library(geosphere)
dist.matrix <- distm(pixels.latlon, grwl.latlon, fun = distHaversine)
# Pick out the indices of the minimum distance
rnum <- apply(dist.matrix, 1, which.min)

At first, this problem was a memory problem because dist.matrix would take 30GB.

A simple solution to overcome this memory problem has been proposed:

library(geosphere)
rnum <- apply(pixels.latlon, 1, function(x) {
  dm <- distm(x, grwl.latlon, fun = distHaversine)
  which.min(dm)
})

Yet, a second problem remains, this solution would take 30-40 min to run.

First idea of improvement

In the same spirit as with this case study in book Advanced R, let us see the source code of the distHaversine function and see if we can adapt it for our particular problem.

library(geosphere)
distHaversine

## function (p1, p2, r = 6378137) 
## {
##     toRad <- pi/180
##     p1 <- .pointsToMatrix(p1) * toRad
##     if (missing(p2)) {
##         p2 <- p1[-1, ]
##         p1 <- p1[-nrow(p1), ]
##     }
##     else {
##         p2 <- .pointsToMatrix(p2) * toRad
##     }
##     p = cbind(p1[, 1], p1[, 2], p2[, 1], p2[, 2], as.vector(r))
##     dLat <- p[, 4] - p[, 2]
##     dLon <- p[, 3] - p[, 1]
##     a <- sin(dLat/2) * sin(dLat/2) + cos(p[, 2]) * cos(p[, 4]) * 
##         sin(dLon/2) * sin(dLon/2)
##     a <- pmin(a, 1)
##     dist <- 2 * atan2(sqrt(a), sqrt(1 - a)) * p[, 5]
##     return(as.vector(dist))
## }
## <bytecode: 0x71c0490>
## <environment: namespace:geosphere>

So, what this code does:

.pointsToMatrix verifies the format of the points to make sure that it is a two-column matrix with the longitude and latitude. Our data is already in this format, we don’t need this here.
it converts from degrees to radians by multiplying by pi / 180.
it computes some intermediate value a.
it computes the great-circle distance based on a.

Knowing that latitude values are between -90° and 90°, you can show that the values of a are between 0 and 1. For these values, dist(a) is in an increasing function of a:

curve(atan2(sqrt(x), sqrt(1 - x)), from = 0, to = 1)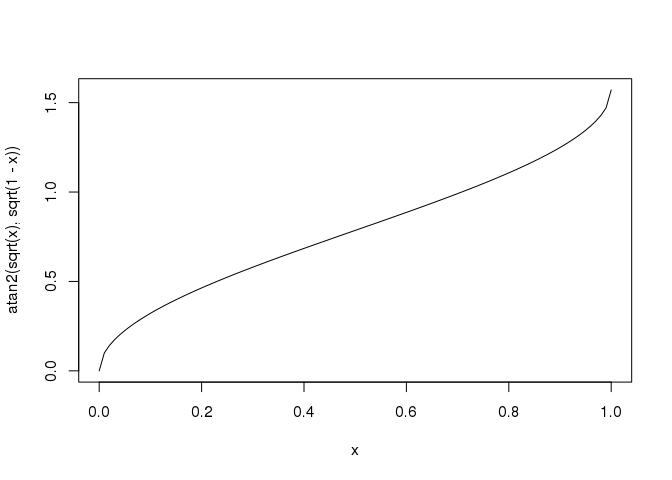

So, in fact, to find the minimum distance, you just need to find the minimum a.

# p1 is just one point and p2 is a two-column matrix of points
haversine2 <- function(p1, p2) {
  
  toRad <- pi / 180
  p1 <- p1 * toRad
  p2 <- p2 * toRad

  dLat <- p2[, 2] - p1[2]
  dLon <- p2[, 1] - p1[1]
  sin(dLat / 2)^2 + cos(p1[2]) * cos(p2[, 2]) * sin(dLon / 2)^2
}

# Test dataset (use smaller size for now)
N <- 200
pixels.latlon <- cbind(runif(N, min = -180, max = -120),
                       runif(N, min = 50, max = 85))
grwl.latlon <- cbind(runif(20000, min = -180, max = -120),
                     runif(20000, min = 50, max = 85))

system.time({
  rnum <- apply(pixels.latlon, 1, function(x) {
    dm <- distm(x, grwl.latlon, fun = distHaversine)
    which.min(dm)
  })
})

##    user  system elapsed 
##   1.852   0.559   2.408

system.time({
  rnum2 <- apply(pixels.latlon, 1, function(x) {
    a <- haversine2(x, grwl.latlon)
    which.min(a)
  })
})

##    user  system elapsed 
##   0.380   0.001   0.383

all.equal(rnum2, rnum)

## [1] TRUE

So, here we get a solution that is 4-5 times as fast because we restricted the source code to our special use case. Still, this is not fast enough in my opinion.

Second idea of improvement

Do you really have to compute distances between all points? For example, if two points are on very different latitudes, does it mean that they are very far from each other?

In a <- sin(dLat / 2)^2 + cos(p1[2]) * cos(p2[, 2]) * sin(dLon / 2)^2, you have a sum of two positive terms. You can deduce that a is always superior to sin(dLat / 2)^2, which is equivalent to 2 * asin(sqrt(a)) is always superior to dLat.

In other terms, for a given point in your matrix, if you have already computed one a0 corresponding to one point in the second matrix, a new point could have its a inferior to a0 only if dLat is inferior to 2 * asin(sqrt(a0)).

So, using a sorted list of all latitudes and with good starting values for a0, you can quickly discard lots of points as being the closest one, just by considering their latitudes. Implementing this idea in R(cpp):

#include <Rcpp.h>
using namespace Rcpp;

double compute_a(double lat1, double long1, double lat2, double long2) {

  double sin_dLat = ::sin((lat2 - lat1) / 2);
  double sin_dLon = ::sin((long2 - long1) / 2);

  return sin_dLat * sin_dLat + ::cos(lat1) * ::cos(lat2) * sin_dLon * sin_dLon;
}

int find_min(double lat1, double long1,
             const NumericVector& lat2,
             const NumericVector& long2,
             int current0) {

  int m = lat2.size();
  double lat_k, lat_min, lat_max, a, a0;
  int k, current = current0;

  a0 = compute_a(lat1, long1, lat2[current], long2[current]);
  // Search before current0
  lat_min = lat1 - 2 * ::asin(::sqrt(a0));
  for (k = current0 - 1; k >= 0; k--) {
    lat_k = lat2[k];
    if (lat_k > lat_min) {
      a = compute_a(lat1, long1, lat_k, long2[k]);
      if (a < a0) {
        a0 = a;
        current = k;
        lat_min = lat1 - 2 * ::asin(::sqrt(a0));
      }
    } else {
      // No need to search further
      break;
    }
  }
  // Search after current0
  lat_max = lat1 + 2 * ::asin(::sqrt(a0));
  for (k = current0 + 1; k < m; k++) {
    lat_k = lat2[k];
    if (lat_k < lat_max) {
      a = compute_a(lat1, long1, lat_k, long2[k]);
      if (a < a0) {
        a0 = a;
        current = k;
        lat_max = lat1 + 2 * ::asin(::sqrt(a0));
      }
    } else {
      // No need to search further
      break;
    }
  }

  return current;
} 

// [[Rcpp::export]]
IntegerVector find_closest_point(const NumericVector& lat1,
                                 const NumericVector& long1,
                                 const NumericVector& lat2,
                                 const NumericVector& long2) {

  int n = lat1.size();
  IntegerVector res(n);

  int current = 0;
  for (int i = 0; i < n; i++) {
    res[i] = current = find_min(lat1[i], long1[i], lat2, long2, current);
  }

  return res; // need +1
}

find_closest <- function(lat1, long1, lat2, long2) {

  toRad <- pi / 180
  lat1  <- lat1  * toRad
  long1 <- long1 * toRad
  lat2  <- lat2  * toRad
  long2 <- long2 * toRad

  ord1  <- order(lat1)
  rank1 <- match(seq_along(lat1), ord1)
  ord2  <- order(lat2)

  ind <- find_closest_point(lat1[ord1], long1[ord1], lat2[ord2], long2[ord2])

  ord2[ind + 1][rank1]
}

system.time(
  rnum3 <- find_closest(pixels.latlon[, 2], pixels.latlon[, 1], 
                        grwl.latlon[, 2], grwl.latlon[, 1])
)

##    user  system elapsed 
##   0.007   0.000   0.007

all.equal(rnum3, rnum)

## [1] TRUE

This is so much faster, because for one point in the first matrix, you just check only a small subset of the points in the second matrix. This solution takes 0.5 sec for N = 2e4 and 4.2 sec for N = 2e5.

4 seconds instead of 30-40 min!

Mission accomplished.

Conclusion

Knowing some maths and some algorithmics can be useful if you are interested in performance.