Scores of PCA

Get the scores of PCA associated with an svd decomposition (class big_SVD).

# S3 method for big_SVD
predict(
  object,
  X = NULL,
  ind.row = rows_along(X),
  ind.col = cols_along(X),
  block.size = block_size(nrow(X)),
  ...
)

Arguments

object: A list returned by big_SVD or big_randomSVD.
X: An object of class FBM.
ind.row: An optional vector of the row indices that are used. If not specified, all rows are used. Don't use negative indices.
ind.col: An optional vector of the column indices that are used. If not specified, all columns are used. Don't use negative indices.
block.size: Maximum number of columns read at once. Default uses block_size.
...: Not used.

Value

A matrix of size \(n \times K\) where n is the number of samples corresponding to indices in ind.row and K the number of PCs computed in object. If X is not specified, this just returns the scores of the training set of object.

Examples

set.seed(1)

X <- big_attachExtdata()
n <- nrow(X)

# Using only half of the data
ind <- sort(sample(n, n/2))

test <- big_SVD(X, fun.scaling = big_scale(), ind.row = ind)
str(test)
#> List of 5
#>  $ d     : num [1:10] 178.5 114.5 91 87.1 86.3 ...
#>  $ u     : num [1:258, 1:10] -0.1092 -0.0928 -0.0806 -0.0796 -0.1028 ...
#>  $ v     : num [1:4542, 1:10] 0.00607 0.00739 0.02921 -0.01283 0.01473 ...
#>  $ center: num [1:4542] 1.34 1.63 1.51 1.64 1.09 ...
#>  $ scale : num [1:4542] 0.665 0.551 0.631 0.55 0.708 ...
#>  - attr(*, "class")= chr "big_SVD"
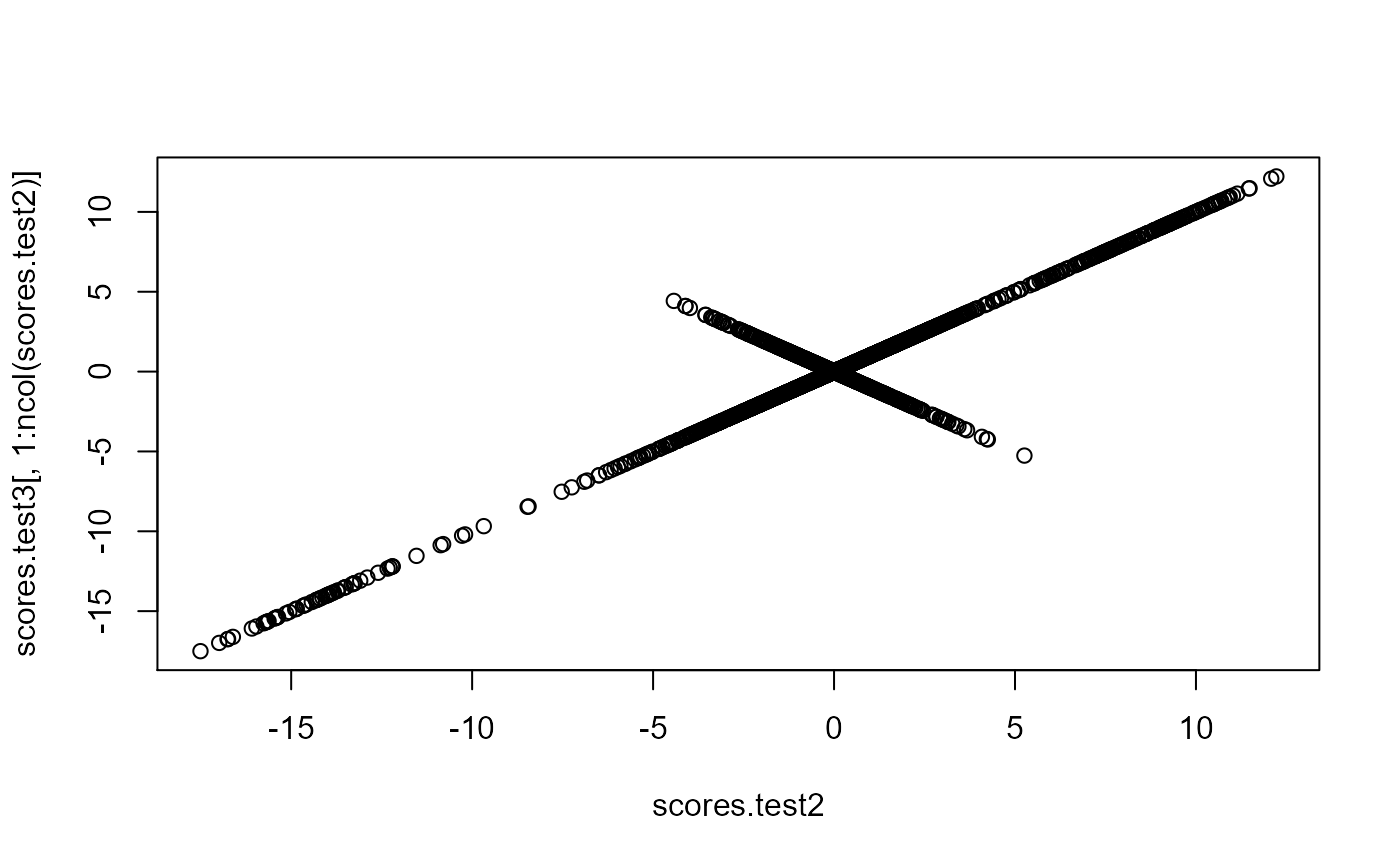
plot(test$u)


pca <- prcomp(X[ind, ], center = TRUE, scale. = TRUE)

# same scaling
all.equal(test$center, pca$center)
#> [1] TRUE
all.equal(test$scale,  pca$scale)
#> [1] TRUE

# scores and loadings are the same or opposite
# except for last eigenvalue which is equal to 0
# due to centering of columns
scores <- test$u %*% diag(test$d)
class(test)
#> [1] "big_SVD"
scores2 <- predict(test) # use this function to predict scores
all.equal(scores, scores2)
#> [1] TRUE
dim(scores)
#> [1] 258  10
dim(pca$x)
#> [1] 258 258
tail(pca$sdev)
#> [1] 3.023287e+00 3.008386e+00 2.990514e+00 2.984375e+00 2.965688e+00
#> [6] 1.130391e-14
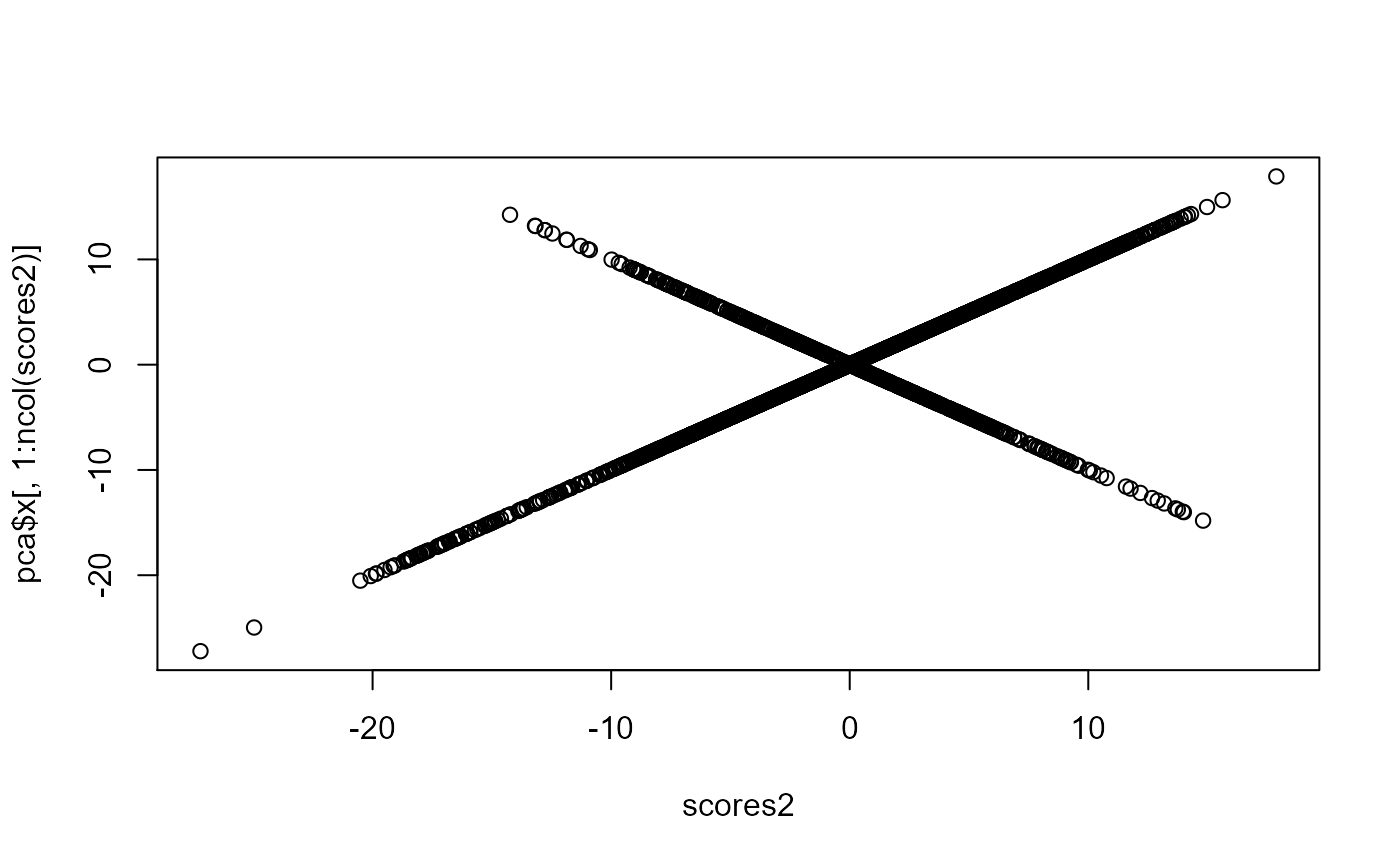
plot(scores2, pca$x[, 1:ncol(scores2)])

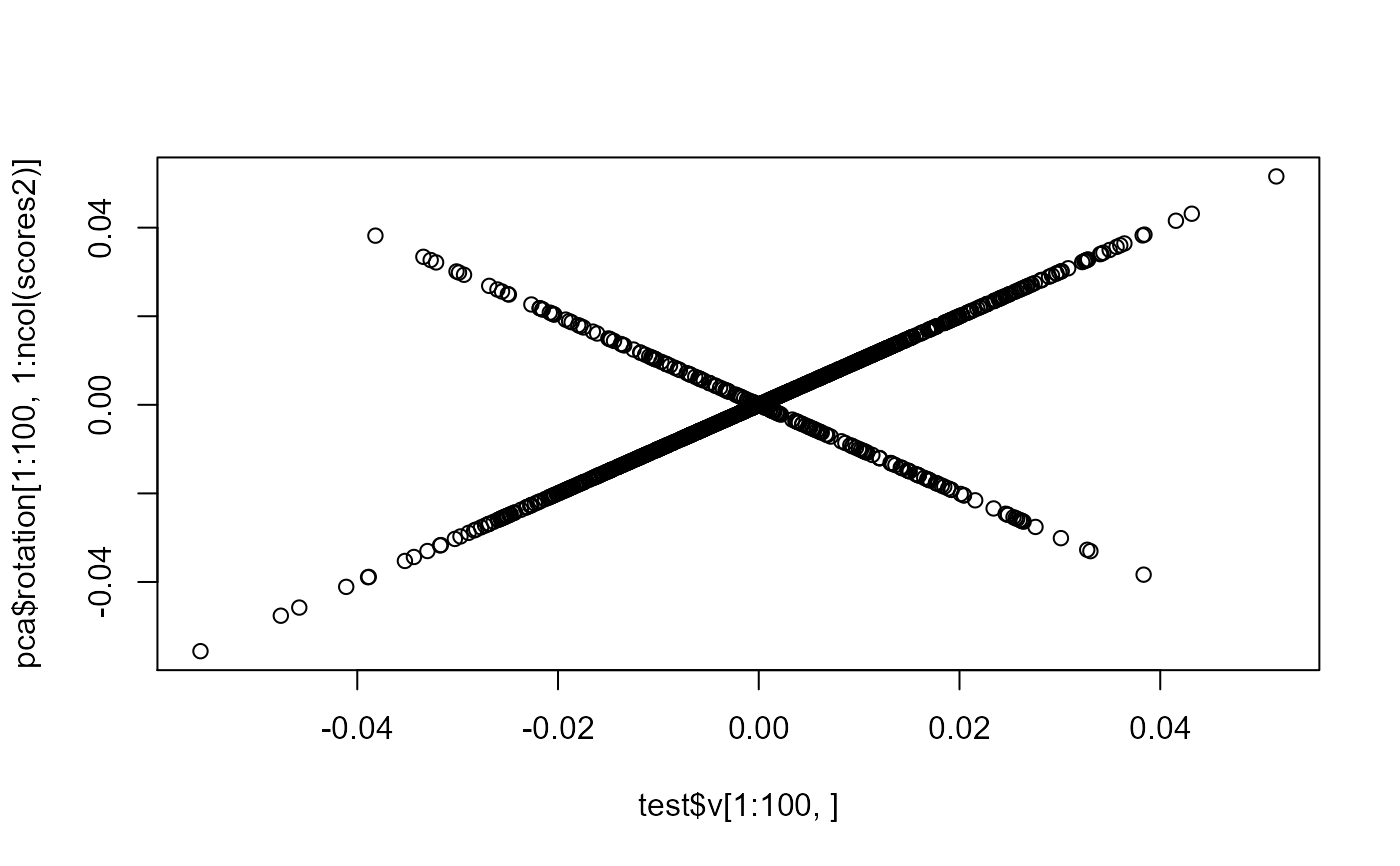
plot(test$v[1:100, ], pca$rotation[1:100, 1:ncol(scores2)])


# projecting on new data
X2 <- sweep(sweep(X[-ind, ], 2, test$center, '-'), 2, test$scale, '/')
scores.test <- X2 %*% test$v
ind2 <- setdiff(rows_along(X), ind)
scores.test2 <- predict(test, X, ind.row = ind2) # use this
all.equal(scores.test, scores.test2)
#> [1] TRUE
scores.test3 <- predict(pca, X[-ind, ])
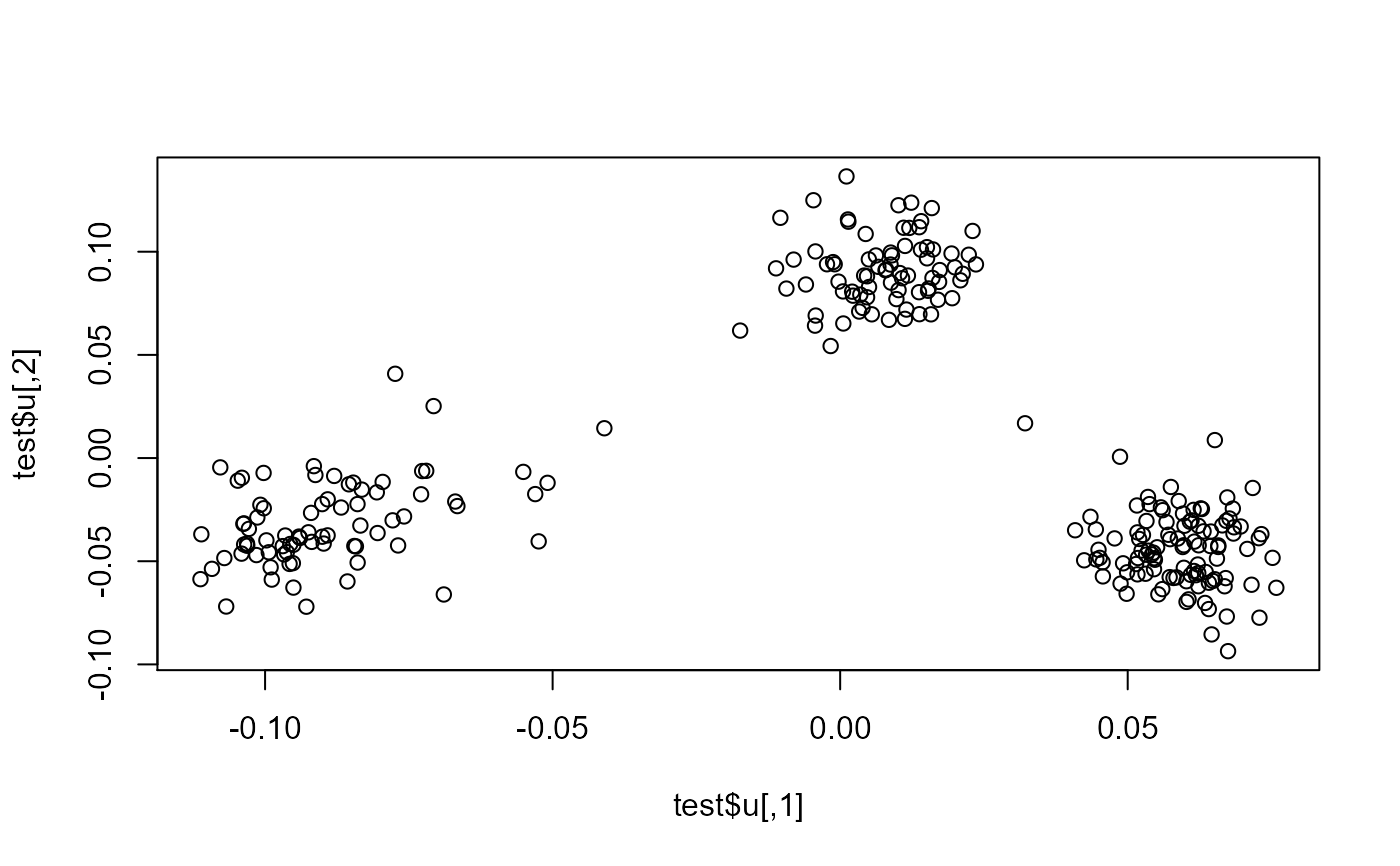
plot(scores.test2, scores.test3[, 1:ncol(scores.test2)])

Arguments

Value

See also

Examples