Binomial(n, p) scaling

Binomial(n, p) scaling where n is fixed and p is estimated.

snp_scaleAlpha(alpha = -1)

snp_scaleBinom(nploidy = 2)

Arguments

alpha

Assumes that the average contribution (e.g. heritability) of a SNP of frequency \(p\) is proportional to \([2p(1-p)]^{1+\alpha}\). The center is then \(2 p\) and the scale is \([2p(1-p)]^{-\alpha/2}\). Default is -1.

nploidy

Number of trials, parameter of the binomial distribution. Default is 2, which corresponds to diploidy, such as for the human genome.

Value

A new function that returns a data.frame of two vectors "center" and "scale" which are of the length of ind.col.

Details

You will probably not use this function as is but as the fun.scaling parameter of other functions of package bigstatsr.

References

This scaling is widely used for SNP arrays. Patterson N, Price AL, Reich D (2006). Population Structure and Eigenanalysis. PLoS Genet 2(12): e190. doi:10.1371/journal.pgen.0020190 .

Examples

set.seed(1)

a <- matrix(0, 93, 170)
p <- 0.2
a[] <- rbinom(length(a), 2, p)
X <- add_code256(big_copy(a, type = "raw"), code = c(0, 1, 2, rep(NA, 253)))
X.svd <- big_SVD(X, fun.scaling = snp_scaleBinom())
str(X.svd)
#> List of 5
#>  $ d     : num [1:10] 22.2 21.6 21.5 21.2 20.8 ...
#>  $ u     : num [1:93, 1:10] 0.0732 -0.0378 -0.0762 0.0364 0.0444 ...
#>  $ v     : num [1:170, 1:10] 0.1075 -0.0331 0.0592 -0.0504 0.1216 ...
#>  $ center: num [1:170] 0.419 0.387 0.301 0.43 0.419 ...
#>  $ scale : num [1:170] 0.576 0.559 0.506 0.581 0.576 ...
#>  - attr(*, "class")= chr "big_SVD"
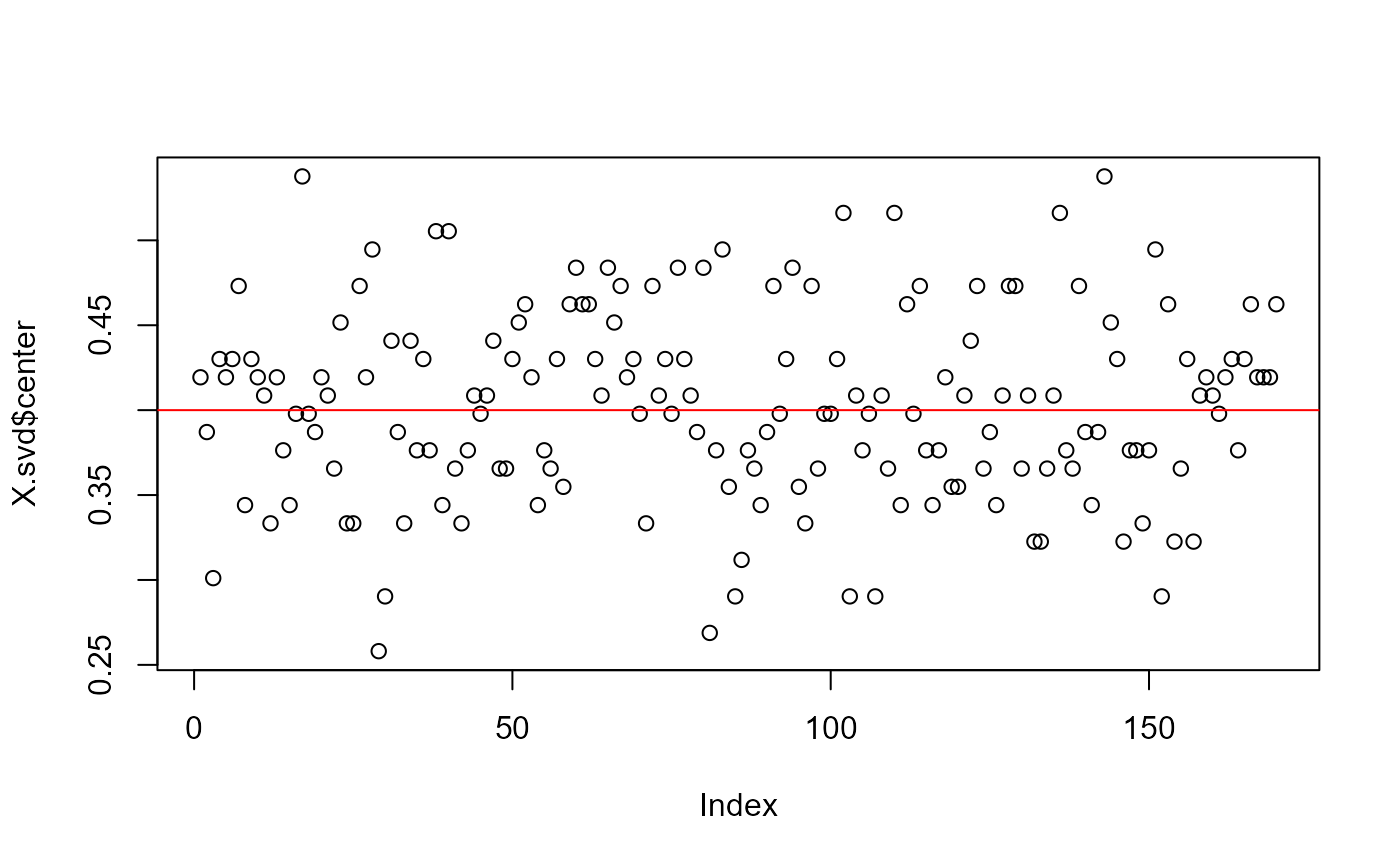
plot(X.svd$center)
abline(h = 2 * p, col = "red")

plot(X.svd$scale)
abline(h = sqrt(2 * p * (1 - p)), col = "red")