Chapter 5 Population structure
5.1 Principal Component Analysis (PCA)
PCA on the genotype matrix can be used to capture population structure. However, PCA can actually capture different kinds of structure (Privé, Luu, Blum, et al., 2020):
population structure (what we want),
Linkage Disequilibrium (LD) structure, when there are too many correlated variants (e.g. within long-range LD regions) and not enough population structure (see this vignette),
relatedness structure, when there are related individuals who usually cluster together in later PCs,
noise, basically just circles when looking at PC scores.
Capturing population structure with PCA is the second main topic of my research work (after polygenic scores).
In Privé et al. (2018), I introduced an algorithm to compute PCA for a
bigSNPobject while accounting for the LD problem by using clumping (not pruning, cf. this vignette) and an automatic detection and removal of long-range LD regions.In Privé, Luu, Vilhjálmsson, et al. (2020), I improved the implementation of the pcadapt algorithm, which detects variants associated with population structure (i.e. some kind of GWAS for population structure).
In Privé, Luu, Blum, et al. (2020), I extended {bigsnpr} to also be able to run PCA on PLINK bed files directly with a small percentage of missing values, and investigated best practices for PCA in more detail.
In Privé, Aschard, et al. (2022) and Privé (2022), I showed how to use PCA for ancestry inference, including grouping individuals in homogeneous ancestry groups, and inferring ancestry proportions from genotype data but also from allele frequencies only (see this vignette).
5.2 Example
There can be many steps to properly perform a PCA, which I try to showcase in the following example. You can find another detailed example of how to conduct a PCA in this vignette.
Let us reuse the data prepared in 4.3.
First, let us get an idea of the relatedness in the data using
#> Loading required package: bigstatsr(NCORES <- nb_cores())
plink2 <- download_plink2("tmp-data")
rel <- snp_plinkKINGQC(plink2, "tmp-data/GWAS_data_sorted_QC.bed",
thr.king = 2^-4.5, make.bed = FALSE, ncores = NCORES)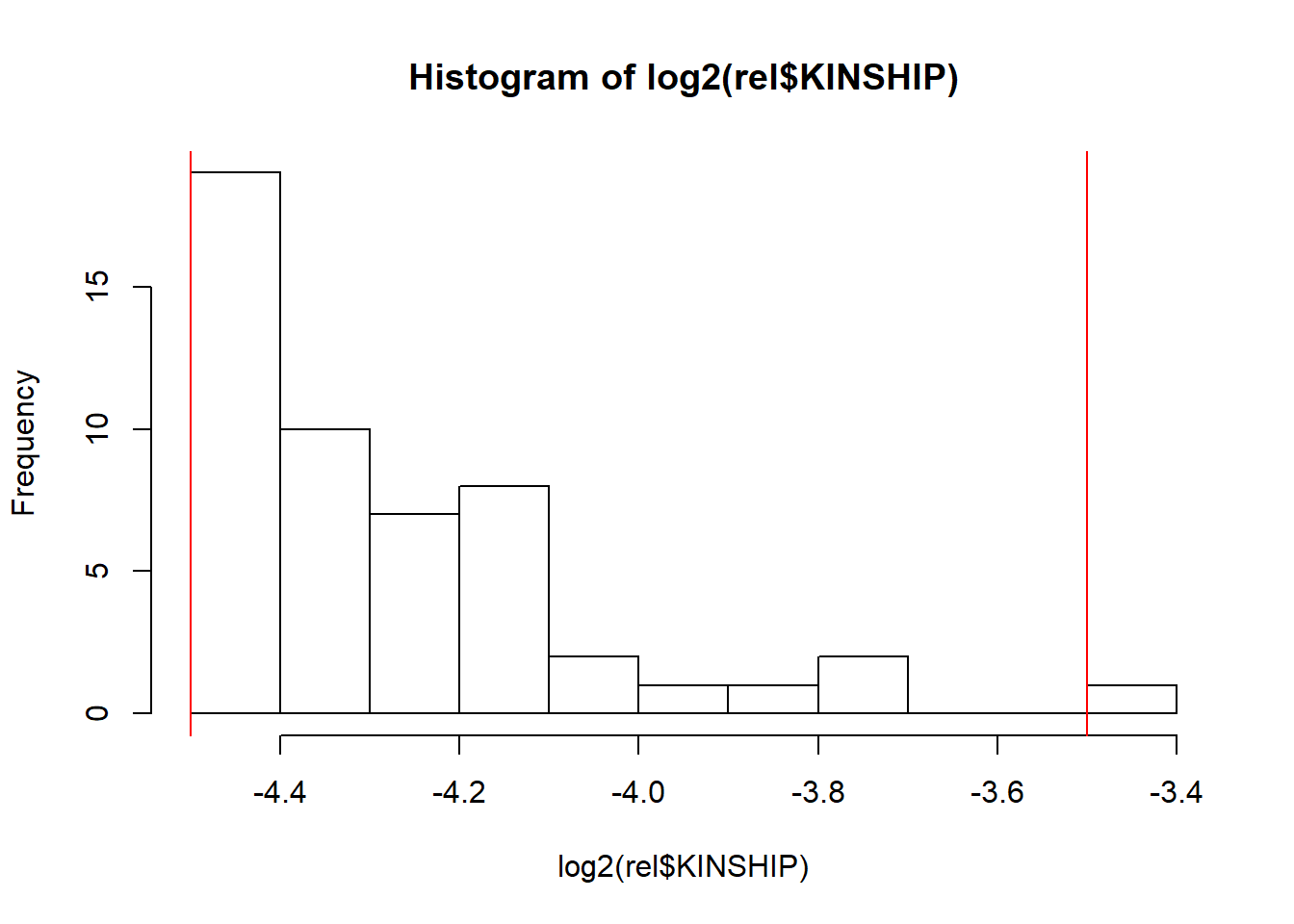
When computing relatedness with KING, LD pruning is NOT recommended. However, it may be useful to filter out some variants that are highly associated with population structure, e.g. as performed in the UK Biobank (Bycroft et al., 2018). For example, see this code.
Relatedness should not be a major issue here. Let us now compute PCs.
All the code that follows could be run on the bigSNP object we made before. Nevertheless, to showcase the bed_* functions here, we will run the following analyses on the bed file directly.
# Memory-map a bed file directly
obj.bed <- bed("tmp-data/GWAS_data_sorted_QC.bed")
str(obj.bed, max.level = 2)#> Reference class 'bed' [package "bigsnpr"] with 13 fields
#> $ bedfile: chr "tmp-data/GWAS_data_sorted_QC.bed"
#> $ extptr :<externalptr>
#> $ .fam :'data.frame': 1401 obs. of 6 variables:
#> $ .map :'data.frame': 404663 obs. of 6 variables:
#> $ prefix : chr "tmp-data/GWAS_data_sorted_QC"
#> $ bimfile: chr "tmp-data/GWAS_data_sorted_QC.bim"
#> $ famfile: chr "tmp-data/GWAS_data_sorted_QC.fam"
#> $ fam :'data.frame': 1401 obs. of 6 variables:
#> $ map :'data.frame': 404663 obs. of 6 variables:
#> $ nrow : int 1401
#> $ ncol : int 404663
#> $ light :Reference class 'bed_light' [package "bigsnpr"] with 5 fields
#> ..and 15 methods, of which 1 is possibly relevant
#> $ address:<externalptr>
#> and 16 methods, of which 2 are possibly relevant:
#> initialize, show#envRefClass# If you expect individuals to all come from the same continent,
# use e.g. k=10, otherwise you can try k=25.
obj.svd <- runonce::save_run(
bed_autoSVD(obj.bed, k = 12, ncores = NCORES),
file = "tmp-data/PCA_GWAS_data.rds")#> user system elapsed
#> 26.58 1.34 139.57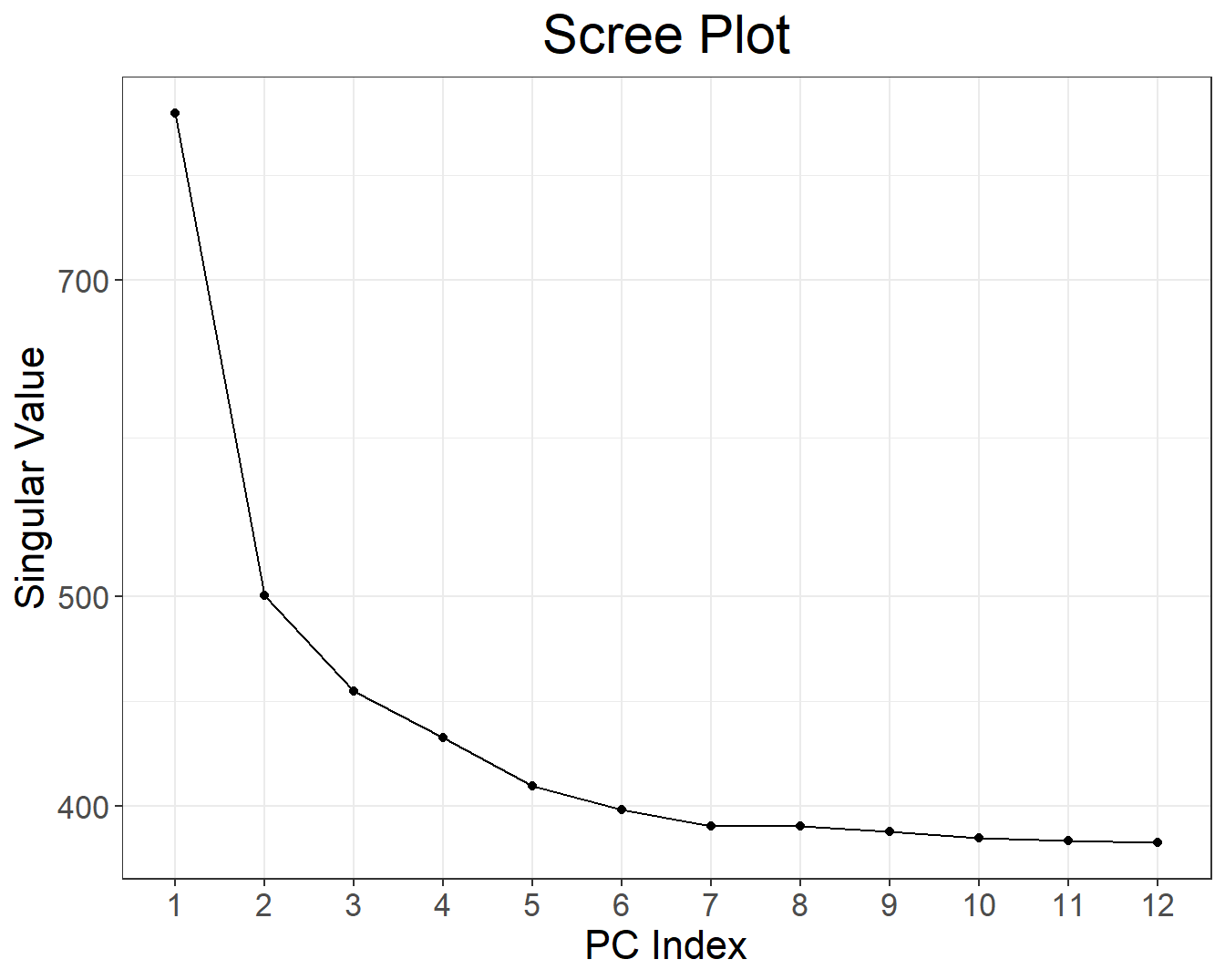
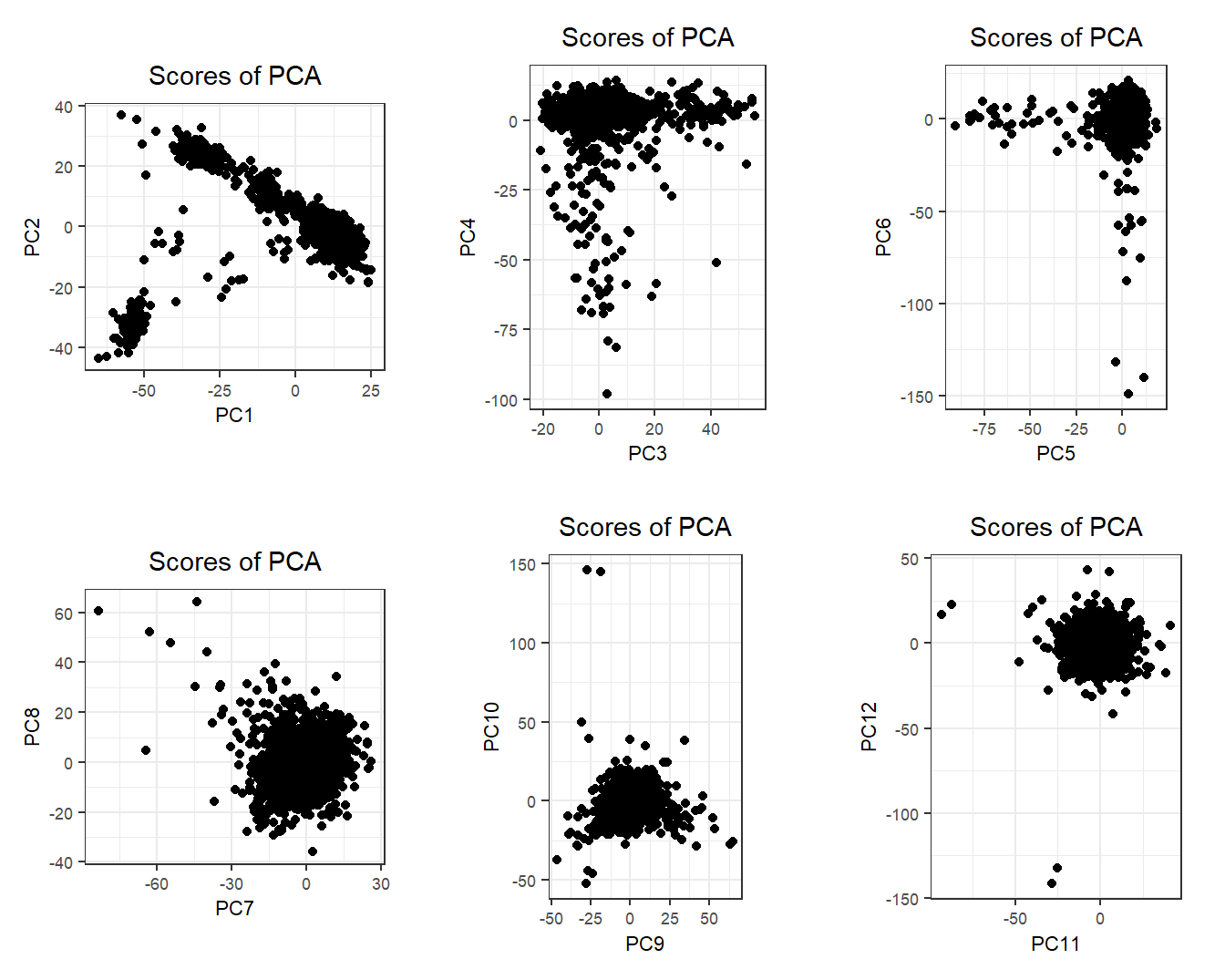
There is some population structure (maybe up to 6 PCs). You should also check loadings to make sure there is no LD structure (peaks on loadings):
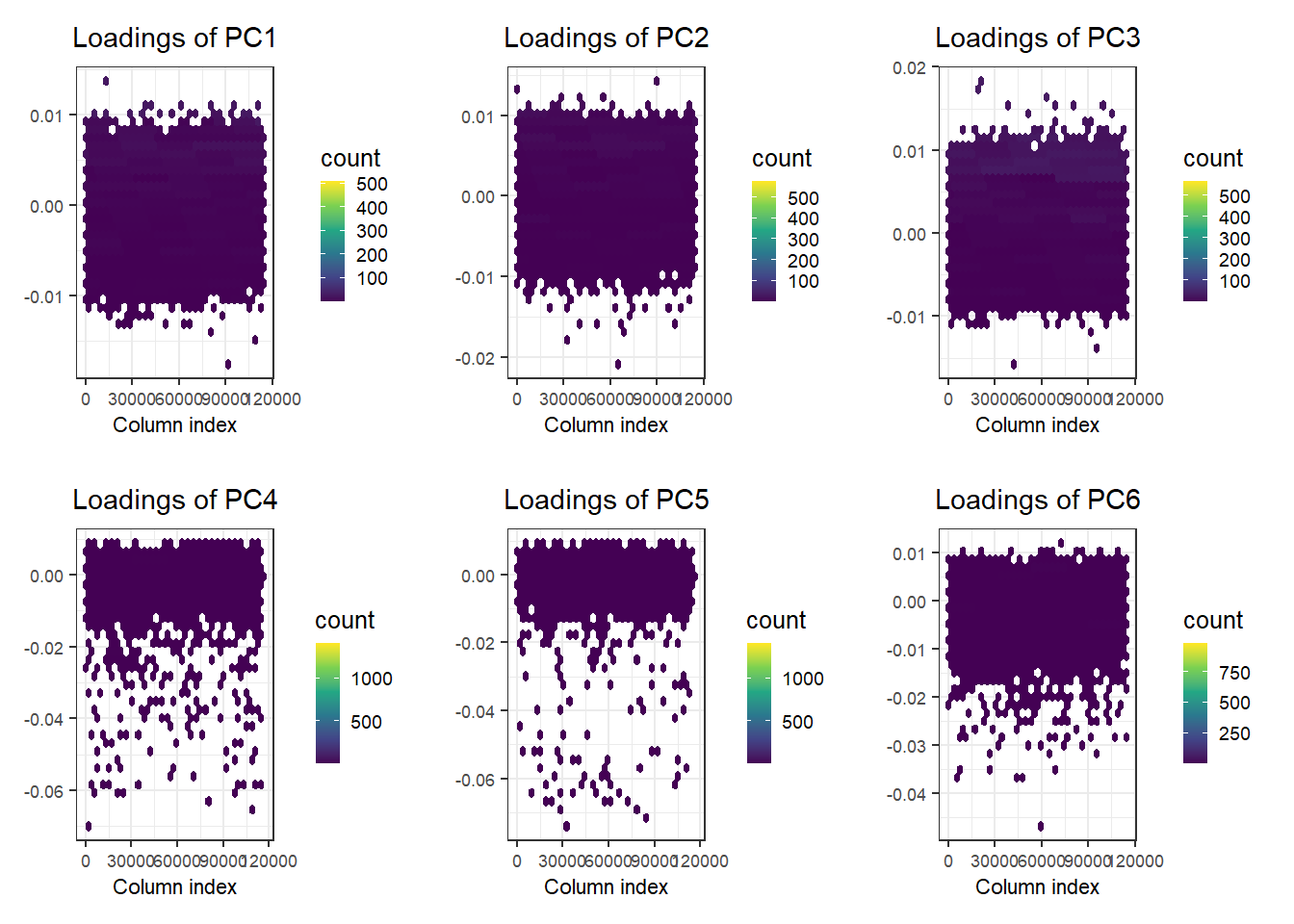
No peaks, but loadings of PC4 and PC5 are a bit odd.
If you expect the individuals to mostly come from one population (e.g. in a national biobank), you can simply use a robust distance to identify a homogeneous subset of individuals, then look at the histogram of log-distances to choose a threshold based on visual inspection (here I would probably choose 4.5).
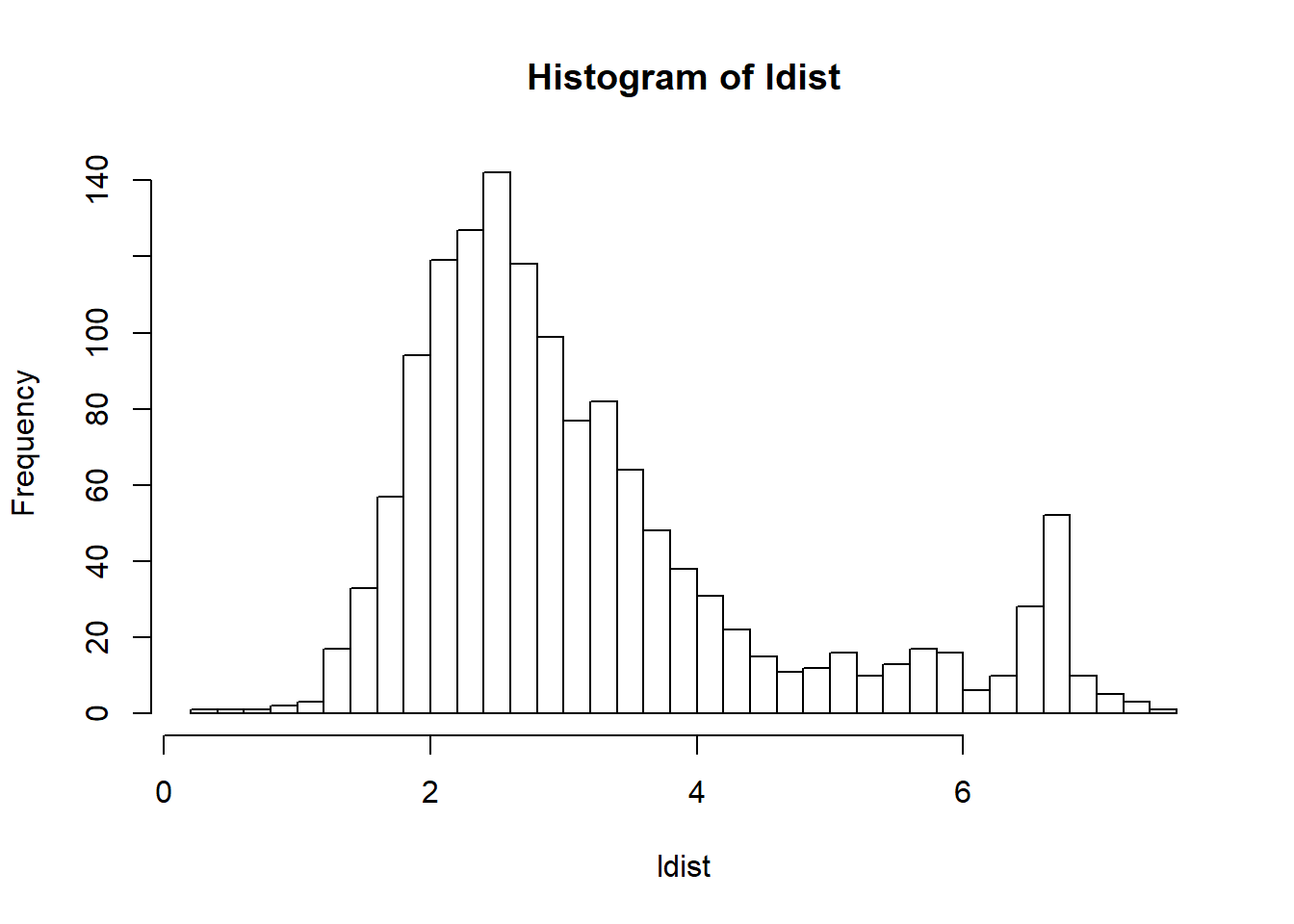
#> Warning: package 'ggplot2' was built under R version 4.2.3source("https://raw.githubusercontent.com/privefl/paper4-bedpca/master/code/plot_grid2.R")
plot_grid2(plotlist = lapply(1:4, function(k) {
k1 <- 2 * k - 1
k2 <- 2 * k
qplot(PC[, k1], PC[, k2], color = ldist, size = I(2)) +
scale_color_viridis_c() +
theme_bigstatsr(0.6) +
labs(x = paste0("PC", k1), y = paste0("PC", k2), color = "log-distance") +
coord_equal()
}), nrow = 2, legend_ratio = 0.2, title_ratio = 0)#> Warning: `qplot()` was deprecated in ggplot2 3.4.0.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.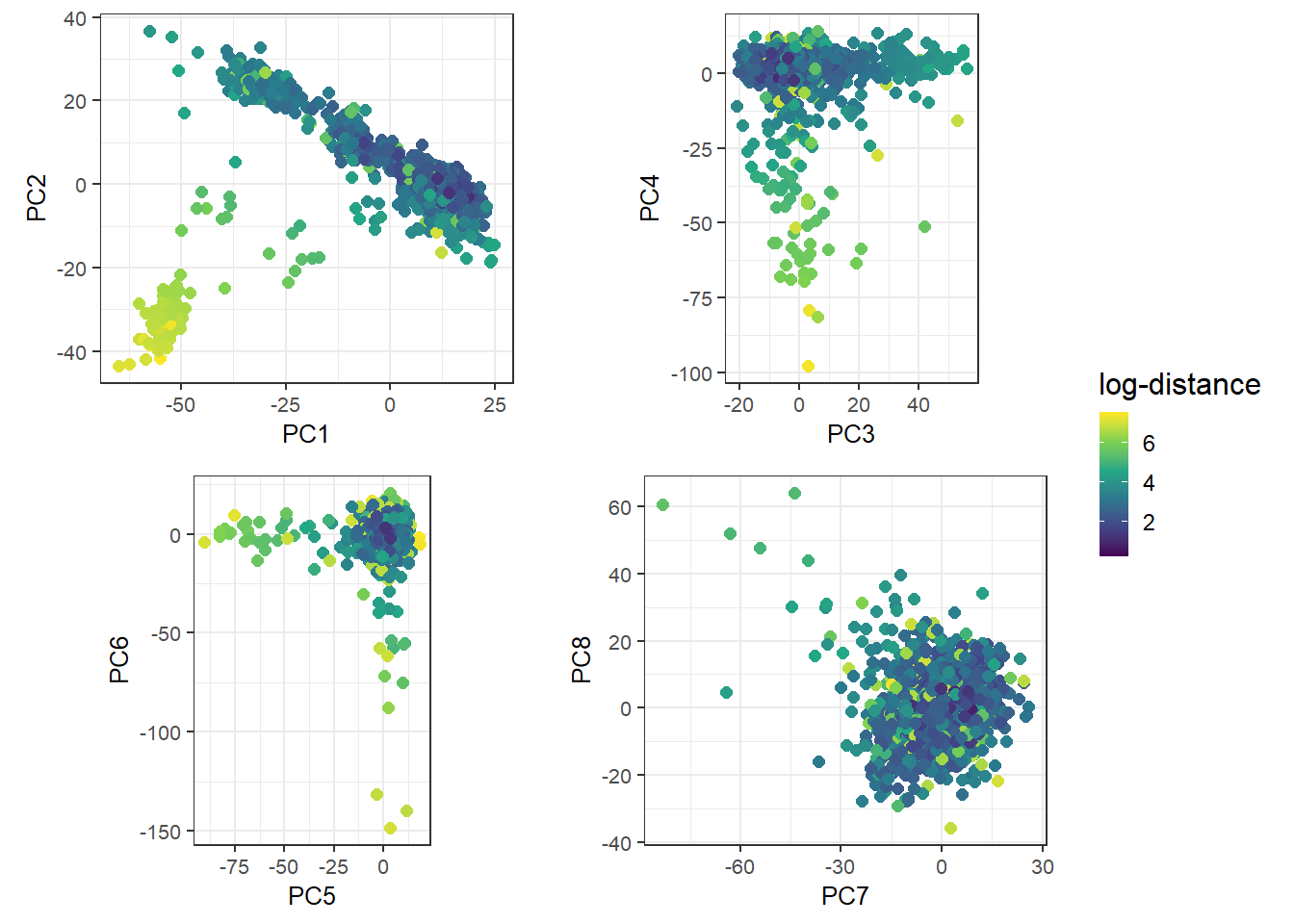
It would be nice if we could get a better sense of the ancestry of these individuals. To achieve this, we can project this data onto the PCA space of many known population groups defined in Privé (2022) (based on the UK Biobank and some individuals from the 1000 Genomes).
all_freq <- bigreadr::fread2(
runonce::download_file(
"https://figshare.com/ndownloader/files/38019027", # subset for the tutorial (46 MB)
# "https://figshare.com/ndownloader/files/31620968", # for real analyses (849 MB)
dir = "tmp-data", fname = "ref_freqs.csv.gz"))
projection <- bigreadr::fread2(
runonce::download_file(
"https://figshare.com/ndownloader/files/38019024", # subset for the tutorial (44 MB)
# "https://figshare.com/ndownloader/files/31620953", # for real analyses (847 MB)
dir = "tmp-data", fname = "projection.csv.gz"))
# coefficients to correct for overfitting of PCA
correction <- c(1, 1, 1, 1.008, 1.021, 1.034, 1.052, 1.074, 1.099,
1.123, 1.15, 1.195, 1.256, 1.321, 1.382, 1.443)#> 'data.frame': 301156 obs. of 26 variables:
#> $ chr : int 1 1 1 1 1 1 1 1 1 1 ...
#> $ pos : int 752566 785989 798959 947034 949608 1018704 1041700 1129672 1130727 1165310 ...
#> $ a0 : chr "G" "T" "G" "G" ...
#> $ a1 : chr "A" "C" "A" "A" ...
#> $ rsid : chr "rs3094315" "rs2980300" "rs11240777" "rs2465126" ...
#> $ Africa (West) : num 0.307 0.179 0.765 0.493 0.437 ...
#> $ Africa (South) : num 0.417 0.233 0.737 0.414 0.352 ...
#> $ Africa (East) : num 0.547 0.493 0.608 0.597 0.261 ...
#> $ Africa (North) : num 0.662 0.645 0.427 0.762 0.319 ...
#> $ Middle East : num 0.794 0.821 0.317 0.886 0.295 ...
#> $ Ashkenazi : num 0.775 0.84 0.203 0.899 0.298 ...
#> $ Italy : num 0.806 0.864 0.243 0.903 0.357 ...
#> $ Europe (South East): num 0.842 0.872 0.201 0.935 0.408 ...
#> $ Europe (North East): num 0.783 0.825 0.203 0.967 0.38 ...
#> $ Finland : num 0.812 0.831 0.224 0.969 0.483 ...
#> $ Scandinavia : num 0.819 0.843 0.228 0.964 0.412 ...
#> $ United Kingdom : num 0.839 0.872 0.2 0.963 0.401 ...
#> $ Ireland : num 0.86 0.887 0.202 0.973 0.387 ...
#> $ Europe (South West): num 0.828 0.867 0.216 0.932 0.347 ...
#> $ South America : num 0.775 0.722 0.324 0.928 0.244 ...
#> $ Sri Lanka : num 0.749 0.753 0.384 0.967 0.293 ...
#> $ Pakistan : num 0.781 0.79 0.347 0.943 0.338 ...
#> $ Bangladesh : num 0.799 0.808 0.33 0.975 0.325 ...
#> $ Asia (East) : num 0.887 0.758 0.319 0.953 0.191 ...
#> $ Japan : num 0.855 0.67 0.397 0.974 0.167 ...
#> $ Philippines : num 0.874 0.845 0.224 0.989 0.212 ...#> 'data.frame': 301156 obs. of 21 variables:
#> $ chr : int 1 1 1 1 1 1 1 1 1 1 ...
#> $ pos : int 752566 785989 798959 947034 949608 1018704 1041700 1129672 1130727 1165310 ...
#> $ a0 : chr "G" "T" "G" "G" ...
#> $ a1 : chr "A" "C" "A" "A" ...
#> $ rsid: chr "rs3094315" "rs2980300" "rs11240777" "rs2465126" ...
#> $ PC1 : num 8.73e-05 5.91e-05 3.81e-05 8.08e-05 9.40e-05 ...
#> $ PC2 : num -1.25e-04 -1.22e-04 1.54e-04 -1.01e-04 2.02e-05 ...
#> $ PC3 : num -5.23e-05 -1.25e-05 1.02e-05 -3.68e-05 1.37e-04 ...
#> $ PC4 : num -3.58e-05 1.01e-06 3.73e-05 -1.24e-05 -1.17e-04 ...
#> $ PC5 : num 2.69e-06 -7.52e-06 4.28e-05 4.53e-05 1.52e-04 ...
#> $ PC6 : num 3.22e-05 2.57e-05 -1.12e-05 1.91e-05 1.76e-04 ...
#> $ PC7 : num -1.64e-05 1.86e-05 -1.21e-04 5.86e-05 1.39e-04 ...
#> $ PC8 : num 2.03e-05 7.16e-05 -1.05e-04 1.00e-05 3.29e-05 ...
#> $ PC9 : num -7.71e-05 -3.57e-05 2.06e-05 -1.10e-05 1.57e-04 ...
#> $ PC10: num 7.27e-06 1.28e-05 1.65e-05 1.68e-05 1.78e-05 ...
#> $ PC11: num 1.35e-04 4.22e-05 -1.22e-05 -5.77e-05 -1.60e-04 ...
#> $ PC12: num -6.57e-05 -4.03e-05 4.44e-05 -2.68e-06 7.79e-05 ...
#> $ PC13: num -6.45e-05 -1.94e-05 5.16e-05 3.27e-05 5.64e-05 ...
#> $ PC14: num -3.13e-05 9.18e-09 -4.06e-05 2.15e-05 -1.59e-04 ...
#> $ PC15: num 1.16e-05 -5.76e-06 1.68e-05 -1.26e-06 -7.81e-05 ...
#> $ PC16: num 6.42e-05 6.47e-05 -4.77e-05 2.51e-05 -9.73e-07 ...Match variants between obj.bed and all_freq using snp_match().
For the variants matched, further remove the variants with more than 5% of missing values.
Click to see solution
# match variants between the two datasets
library(dplyr)
matched <- obj.bed$map %>%
transmute(chr = chromosome, pos = physical.pos, a1 = allele1, a0 = allele2) %>%
mutate(beta = 1) %>%
snp_match(all_freq[1:5]) %>%
print()#> chr pos a0 a1 beta _NUM_ID_.ss rsid _NUM_ID_
#> 1 1 752566 G A -1 2 rs3094315 1
#> 2 1 785989 T C -1 4 rs2980300 2
#> 3 1 798959 G A 1 5 rs11240777 3
#> 4 1 947034 G A -1 6 rs2465126 4
#> 5 1 949608 G A 1 7 rs1921 5
#> 6 1 1018704 A G -1 8 rs9442372 6
#> [ reached 'max' / getOption("max.print") -- omitted 301150 rows ]# further subsetting on missing values
counts <- bed_counts(obj.bed, ind.col = matched$`_NUM_ID_.ss`, ncores = NCORES)
hist(counts[4, ])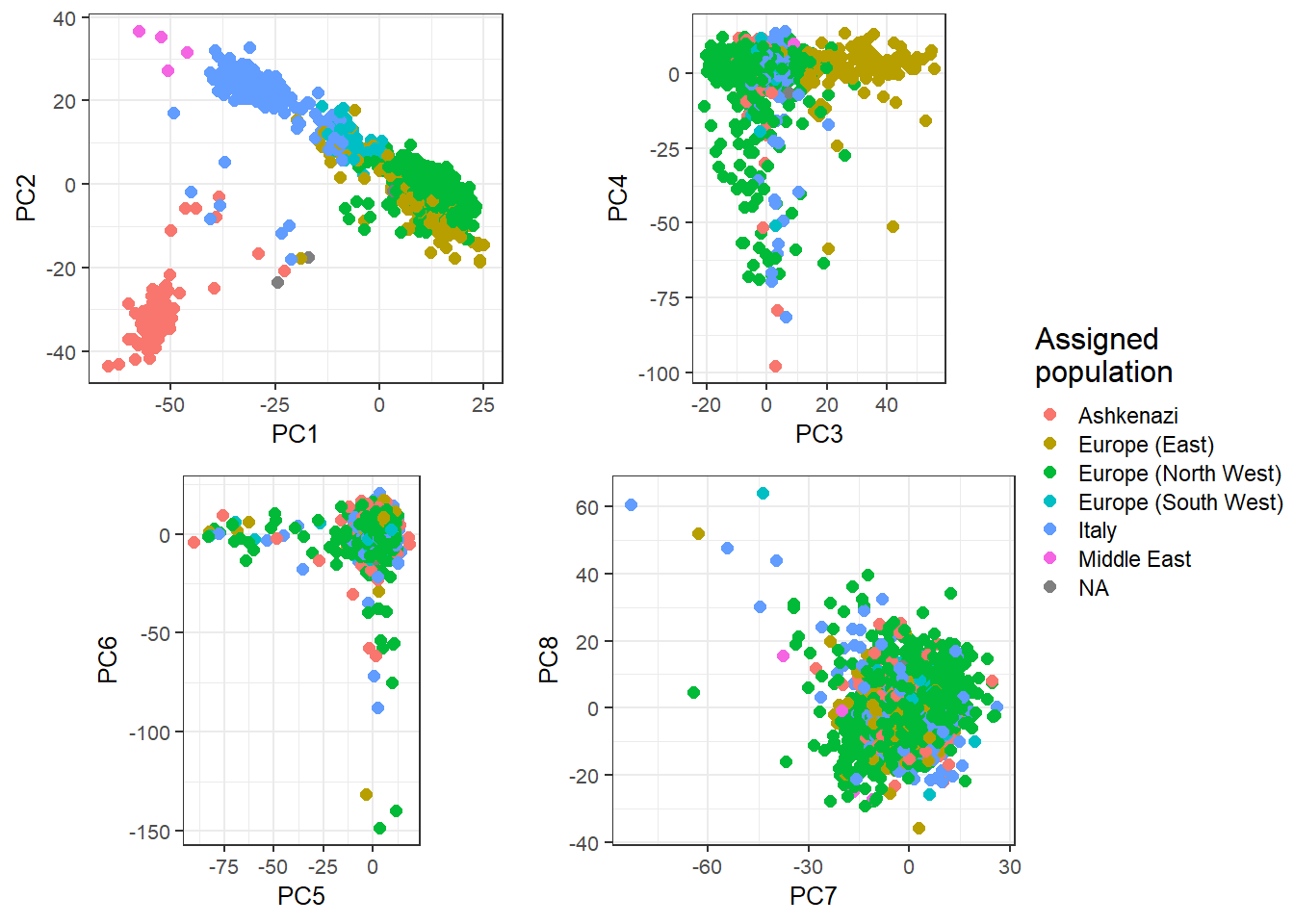
# projection matrix
proj_mat <- as.matrix(projection[matched2$`_NUM_ID_`, -(1:5)])
# reference allele frequencies
ref_mat <- as.matrix(all_freq [matched2$`_NUM_ID_`, -(1:5)])
# centers of reference populations in the PCA
all_centers <- crossprod(ref_mat, proj_mat)# project individuals (divided by 2 -> as AF) onto the PC space
all_proj <- apply(sweep(proj_mat, 2, correction / 2, '*'), 2, function(x) {
bed_prodVec(obj.bed, x, ind.col = matched2$`_NUM_ID_.ss`, ncores = NCORES,
# scaling to get G if beta = 1 and (2 - G) if beta = -1
center = 1 - matched2$beta, scale = matched2$beta)
})The correction factors are needed when projecting new individuals onto a PCA space to correct for the shrinkage that happens due to “overfitting” of the PCA. This happens particularly when the number of individuals used to derive the PCA is smaller than the number of variables. The amount of correction needed increases for later PCs. You can have a look at Privé, Luu, Blum, et al. (2020) to read more about this.
Note that the provided correction is specific to the PC loadings I provide, so that you don’t need to recompute it. It is based on the ratio between the projections using a method that corrects for this shrinkage and the simple projections (simply multiplying by the loadings on the right).
In Privé, Aschard, et al. (2022), I have showed that distances in the PCA space are approximately proportional to \(F_{ST}\) (a genetic distance). So I recommend using distances in the PCA space to assign individuals to clusters. So that clusters remain somewhat homogeneous, a maximum distance can be set based on proportionality with a chosen \(F_{ST}\) threshold.
We can then assign each individual to their closest center:
# distance of individuals from each reference population (the center)
all_sq_dist <- apply(all_centers, 1, function(one_center) {
rowSums(sweep(all_proj, 2, one_center, '-')^2)
})
thr_fst <- 0.002 # you can adjust this threshold
thr_sq_dist <- max(dist(all_centers)^2) * thr_fst / 0.16
# gather some groups
group <- colnames(all_freq)[-(1:5)]
group[group %in% c("Scandinavia", "United Kingdom", "Ireland")] <- "Europe (North West)"
group[group %in% c("Europe (South East)", "Europe (North East)")] <- "Europe (East)"
# assign to closest cluster, when close enough
cluster <- apply(all_sq_dist, 1, function(sq_dist) {
ind <- which.min(sq_dist)
if (sq_dist[ind] < thr_sq_dist) group[ind] else NA
})
table(cluster, exclude = NULL) # 3 NAs -> almost all assigned#> cluster
#> Ashkenazi Europe (East) Europe (North West)
#> 110 148 872
#> Europe (South West) Italy Middle East
#> 45 219 4
#> <NA>
#> 3plot_grid2(plotlist = lapply(1:4, function(k) {
k1 <- 2 * k - 1
k2 <- 2 * k
qplot(PC[, k1], PC[, k2], color = cluster, size = I(2)) +
theme_bigstatsr(0.6) +
labs(x = paste0("PC", k1), y = paste0("PC", k2), color = "Assigned group") +
coord_equal()
}), nrow = 2, legend_ratio = 0.25, title_ratio = 0)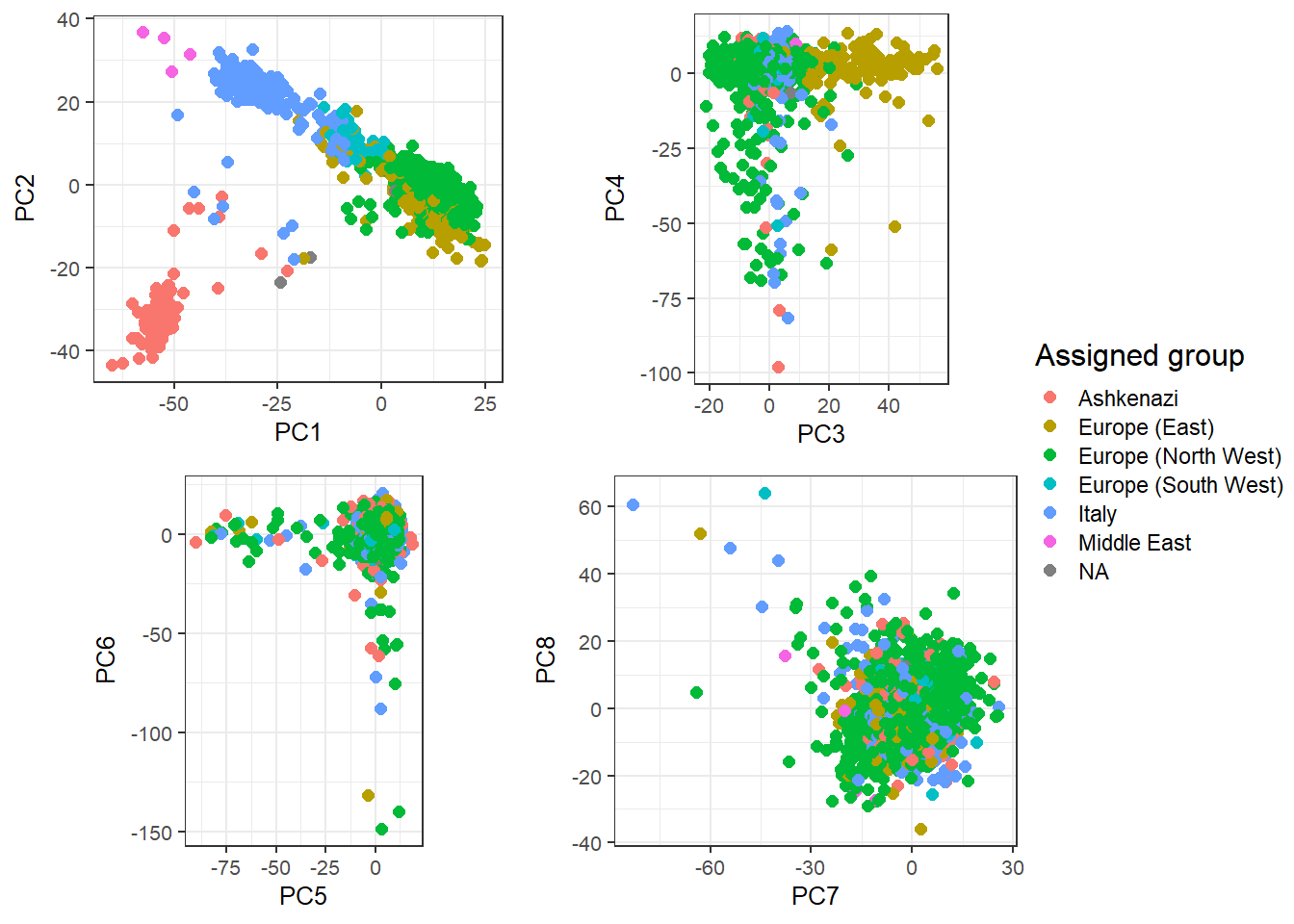
These are mostly European individuals. PC4 is definitively a bit odd.
Try to find out what’s going on with PC4.
Adapt all the previous code to rerun it on the bigSNP object we made before (instead of the bed object we have used here).